Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 04. 2011 15:32
#3 05. 04. 2011 16:45
- nie_som_matematik


- Příspěvky: 63
- Reputace: 0
Re: Neurčitý integrál
↑ Rumburak:
Ďakujem za vodítko, ale ešte by som chcel poprosiť, či by ste mi to nepomohli vyriešiť úplne do konca? Pozerám sa do zbierky príkladov a je to typ príkladov, ktoré sme neriešili, ale na zápočtovej písomke boli.
Vopred ďakujem a vážim si ochotu.
Offline
#4 05. 04. 2011 18:08
Re: Neurčitý integrál
při substituci  formálně dostaneme
formálně dostaneme  a
a

až nakonec mi vyšlo: http://www.wolframalpha.com/input/?i=di … 29%29%2F16
Hádám, že měl Rumburak na mysli nějaký elegantnější postup :-)
Offline
#5 06. 04. 2011 08:17
Re: Neurčitý integrál
na riesenie integralov a podobnych je na webe super tool:
http://www.wolframalpha.com/
Offline
#6 06. 04. 2011 09:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál
↑ overcat:
děkuji, je to uvedeno v úvodním tématu sekce VŠ, odkaz má kolegyňka ↑ claudia: v příspěvku, všude doporučuji MAW, ale jinak takovým zavedením strojů se z integrování stala "riadná nuda" (c)
Zde se mi zda možné použit per partes  ,
,  po úpravách se dostávám na metodu "něco - něco jiného" a ještě bude třeba použit takové integrování.
po úpravách se dostávám na metodu "něco - něco jiného" a ještě bude třeba použit takové integrování.
Určitě jsem to v takto brzkých hodinách překombinovala :-)
Zdravím v tématu a nejen.
Offline
#7 06. 04. 2011 09:13 — Editoval Rumburak (06. 04. 2011 10:05)
Re: Neurčitý integrál
↑ claudia:
Ahoj :-) a díky za podrobnosti k té substituci. Mně k ní přilákalo možné využití vztahů
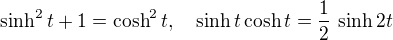 .
.
S ohledem na třetí řádek odzdola v Tvém výpočtu (↑ claudia:) tedy stačí (po substituci u = 2t) provést úpravu 
a dopočítat to už opravdu není těžké, vystačíme se základními znalostmi a proto doufám, že to zvládne i kolega
↑ nie_som_matematik: :-).
Offline

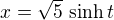 (viz hyperbolické funkce).
(viz hyperbolické funkce).