Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 07. 2011 10:20
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
kde sem udělala chybu? [rovnice]
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
- (téma jako vyřešené označil(a) Alenka.Janská)
#3 13. 07. 2011 10:39 — Editoval Cheop (13. 07. 2011 10:43)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská:
Společný jmenovatel zlomků je 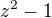 , ale protože ty máš zlomky
, ale protože ty máš zlomky  a
a 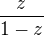 jejich společný jmenovatel je:
jejich společný jmenovatel je: 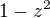
musíš zlomek 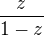 vynásobit výrazem
vynásobit výrazem 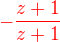 , abys dostala společný jmenovatel
, abys dostala společný jmenovatel 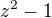
Dostaneš tedy:
Nikdo není dokonalý
Offline
#4 13. 07. 2011 10:50
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská:
Na druhém řádku jsi znovvu udělala tutéž chybu, na kterou jsem Tě upozorňoval už zde: ↑↑ Rumburak:.
Musíš pochopit, že 1 - z = - (z - 1) a dávat si na to pozor.
Obecná doporučení:
1) Důležité je vyhradit si na práci čas a klidné místo, kde Tě nebude nikdo a nic rušit, a předem si připravit tužku a stoh čistého papíru.
2) Zvykni si zadání úlohy i průběžné výpočty zapisovat s co nejleší úpravou, aby byly přehledné a Tvoji pozornost neodpoutávalo jejich
zpětné "luštění".
3) Výpočty prováděj s maximálním soustředěním a po malých krocích.
4) Každý problémový příklad si spočítej několikrát za sebou a i později se k němu občas vrať, dokud ho nebudeš mít zvládnutý zcela bezpečně.
Naučit se suverénně spočítat jeden příklad Ti dá více, než spočítat 10 příkladů polovičatě a s chybami.
5) Nemá také smysl těkat z jednoho tématického okruhu do druhého. Když se dobře naučíš základní algebru (tou bych začal), i další partie včetně
geometrie Ti pak půjdou lépe.
Offline
#5 13. 07. 2011 10:53
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
Re: kde sem udělala chybu? [rovnice]
↑ Cheop:
já už nmičemu nerozumim...
taktže bych za to lomítko musela napsal (1 + z) . (1 - z)
nebo co mám napsat za to lomítko, co určuje o co jde k roznásobení
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
#6 13. 07. 2011 10:55
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
Re: kde sem udělala chybu? [rovnice]
↑ Rumburak:
1 - z = - (z - 1)
tomu fakt nerozumím
přece - (z -1) mi fakt dá po přenásobení -z + 1 což je JINÁ HODNOTA než 1 - z
co z toho teda vyplívá?
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
#7 13. 07. 2011 10:59 — Editoval Cheop (13. 07. 2011 11:08)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská:
Zlomek 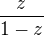 je ten stejný zlomek jako:
je ten stejný zlomek jako: 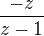 jmenovatel i čitatel je výnásoben číslem (-1)
jmenovatel i čitatel je výnásoben číslem (-1)
Celé zadaní tvého příkladu: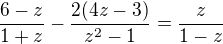 můžeš upravit na:
můžeš upravit na: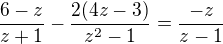 a z toho už vidíš, kterými výrazy musíš rozšířit zlomky
a z toho už vidíš, kterými výrazy musíš rozšířit zlomky  resp.
resp. 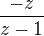 , abys dostala společný jmenovatel
, abys dostala společný jmenovatel 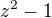 při vědomí toho, že
při vědomí toho, že 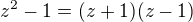
Nikdo není dokonalý
Offline
#8 13. 07. 2011 11:20
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská:
To si, prosím, rozmyslete.
Offline
#9 13. 07. 2011 11:28
Re: kde sem udělala chybu? [rovnice]
přece - (z -1) mi fakt dá po přenásobení -z + 1 což je JINÁ HODNOTA než 1 - z
co z toho teda vyplívá?
Hodnota -z+1=1-z, nevím co z to je na plivání, ale vyplývá z toho, že výrazy jsou stejné.
Offline
#10 13. 07. 2011 11:41
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
Re: kde sem udělala chybu? [rovnice]
já už nic nechápu....
vyřeště mi ten příklad jako vzor, a já na to aplikuji vaše poučky
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
#12 13. 07. 2011 12:10 — Editoval Cheop (13. 07. 2011 13:05)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská: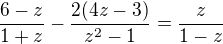
1) Určíme podmínky
Aby měla rovnice smysl potom jmenovatel zlomků musí být různý od nuly (nulou nelze dělit) tedy
a) 
b) 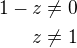
c) 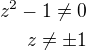

Rovnice má nekonečně mnoho řešení
Rovnice platí pro jakékoliv reálné číslo z s vyjímkou 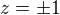
Řešení: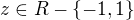
Nikdo není dokonalý
Offline
#13 13. 07. 2011 12:22
Re: kde sem udělala chybu? [rovnice]
↑ Alenka.Janská:
Pro sčítání platí komutativní zákon: jsou-li A , B libovolná čísla, potom A + B = B + A .
Příklad : 2 + 6 = 8 , 6 + 2 = 8 aj.
Spaciálně pro A = -z, B = 1: (-z) + 1 = 1 + (-z) , kde úsporněji zapisujeme levou stranu ve tvaru -z + 1, pravou stranu ve tvaru 1 - z.
Celkem: -z + 1 = 1 - z, obecně : -C + D = D - C .
Offline