Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 06. 11. 2011 00:46 — Editoval vanok (06. 11. 2011 00:46)
Re: najkrajsia teorema
Dnes mam chut vam hovorit podla mna o krasnej teorii
"integral Kurzweil-Henstock"
alebo aj
"integral Henstock-Kurzweil"
Je to revolucny krok vo vyvoji teorii o integraloch.
Tu si osviezte vase myslienky o tom.
http://en.wikipedia.org/wiki/Henstock%E … l_integral
Ja som hladal na internete kto je(bol?) tento velky cesky matematik Jaroslav Kurzweil, ktory objavil tento integral v 1957 a ktory bol rozvynuty anglickym matematikom Ralph Henstock.
a nasiel len toto
http://cs.wikipedia.org/wiki/Jaroslav_Kurzweil
Napiste sem vsetci co nieco o nom viete, jeho zivotopis, alebo aj ankdoty z jeho zivota aby sa na takehoto mimoriadneho cloveka nezabudlo!
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#27 07. 11. 2011 11:39
Re: najkrajsia teorema
Jaroslav Kurzweil je ozaj taky clovek ze nikto o nom nic nevie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#28 07. 11. 2011 12:00
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: najkrajsia teorema
↑ vanok:
Já matematiku nestuduji, takže o něm opravdu mnoho nevím, vím jen, že existuje jeho integrál. Vím ale, že se tu o něm na fóru už jednou mluvilo.
Offline
#29 07. 11. 2011 14:07 — Editoval Rumburak (07. 11. 2011 14:09)
Re: najkrajsia teorema
↑ vanok:
Ahoj,
u prof. Jaroslava Kurzweila jsem kdysi absolvoval universitní semestrální kurs z obyčejných diferenciálnách rovnic.
Pan profesor byl na fakutě (MFF UK) slavný - a to nejen mezi studenty, ale i mezi ostatními vyučujícími - m.j. tím, že
jeho přednášky byly velmi náročné na sledování, což mohu jen potvrdit, protože pravidelně už po několika minutách
většina z nás - studentů třetího ročníku - přestala chápat, o co jde, neb výklad byl více o různých nuancích a zajímavých
singularitách než o standardní látce pro začátečníky v této oblasti, jimiž jsme byli. Kdo se učil dopředu ze skript, měl
samozřejmě velkou výhodu a přednáška mu dala to, co už nebylo ve skriptech, ale kolik procent studentů tak činí ?
Jinak to byla pohoda, pana profesora jsem vždy vnímal jako velmi milého člověka a rád na něho vzpomínám.
Offline
#30 09. 11. 2011 16:14
Re: najkrajsia teorema
nevahajte a pokracujte zo zivotopisom Jaroslava Kurzweila.
A teraz pekna az magicky pekna TEOREMA SARKOVSKEHO (slaba forma)
Ak spojita funkcia z nejakeho intervalu I do sameho seba ma jeden bod periody 3, tak potom ma bod periody n, pre kazde n.
Mozno ju poznate v heslovytej forme
3-cycle implikuje chaos
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#31 13. 11. 2011 23:05
Re: najkrajsia teorema
↑ vanok:,
Na tuto peknu teoremu nie je tu ziadne echo :-(
A cakam aj na vase...
Ja ich mam dost vela, co sa mi pacia; a vy?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#32 13. 11. 2011 23:32
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: najkrajsia teorema
Vím, že mě velmi zaujalo tvrzení, že neabsolutně konvergentní posloupnost lze přerovnat tak, že konverguje k libovolnému číslu. Zpravidla poté, co člověk vidí důkaz, přestane být tvrzení tak zajímavé, ale toto byla z mnoha věcí, kde počatční "odhad" selhal. Takové nečekané věci mám rád.
"Máte úhel beta." "No to nemám."
Offline
#33 20. 11. 2011 13:56
Re: najkrajsia teorema
Ahoj ↑ check_drummer:,
Zatial nie je nas tu vela, co sa odvazuju tu nieco napisat.
Aj ja i myslim ze tvoja veta je fascinujuca...
A teraz dalsy pekny vysledok:
Teorema trisekcie od Morley
http://en.wikipedia.org/wiki/Morley%27s … or_theorem
Viem ze to kazdy pozna ale tak ci tak je ozaj pekna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#34 20. 11. 2011 16:55
Re: najkrajsia teorema
Pre každú číselnú sústavu so základom z>2 existuje jediná dvojica dvojmiestných čísel A, B, ktoré sa líšia iba poradím svojich číslic a majú tú vlasnosť, že kvadratická rovnica x^2 - Ax + B = 0 má dvojnásobný koreň.
Toto sa mi fakt páči :)
1^6 - 2^6 + 3^6 = 666
Offline
#35 21. 11. 2011 11:32 — Editoval Rumburak (07. 12. 2011 15:01)
Re: najkrajsia teorema
↑↑ vanok:
Při volbě nekrásnější matematické věty bych asi hlasoval pro známý Eulerův vzorec
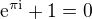 ,
,
který třemi základními operacemi (jimiž jsou sčítání, násobení, umocňování) spojuje pět nejdůležitějších číselných konstant.
I když je i mnoho dalších pěkných vět, třeba Brouwerova věta o pevném bodě a j., takže volba není lehká.
Offline
#37 21. 11. 2011 14:43
Re: najkrajsia teorema
Já bych přidal Taylorovu větu (Taylorův rozvoj). Je velice pozoruhodné, že stačí mít k dispozici derivace funkce pouze v jednom jediném bodě a pomocí nich lze určit hodnotu funkce v bodech ostatních.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#38 07. 12. 2011 12:16
Re: najkrajsia teorema
Dalsia "najkajsia" teorema.
Je znama pod menom
Grand théorème de Poncelet
alebo este
Poncelet's porism
Dokaz najdete napriklad tu
http://en.wikipedia.org/wiki/Poncelet%27s_porism
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#40 08. 12. 2011 03:05
Re: najkrajsia teorema
Ahoj ↑ L1ebeq:,
Mas riesenie na tento pekny enigmaticky problem?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#41 08. 12. 2011 06:54
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: najkrajsia teorema
↑ L1ebeq:
K 1) bych si tipl, že bude "ráno moudřejší večera" (IQ AM vs. PM.) :-)
K 2) po bitvě je každý generál? :-)
"Máte úhel beta." "No to nemám."
Offline
#42 08. 12. 2011 11:02
Re: najkrajsia teorema
↑ check_drummer: Úžasné, navrhujem Ťa na cenu J.F.Champolliona :-)
http://cs.wikipedia.org/wiki/Jean-Fran% … hampollion
Offline
#43 08. 12. 2011 11:47 — Editoval vanok (08. 12. 2011 11:47)
Re: najkrajsia teorema
Pekne riesenie, ↑ check_drummer:,
A ako sa vam paci "Grand théorème de Poncelet" re]p240865|vanok[/re]?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#44 09. 12. 2011 17:48
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Musím říct, že po zběžném zhlédnutí důkazu asi v tuto chvíli nemám dostatečnou znalost teorie v něm obsažené...
"Máte úhel beta." "No to nemám."
Offline
#45 10. 12. 2011 00:18
Re: najkrajsia teorema
Ahoj ↑ check_drummer:,
To je pravda ze niektore pekne teoremy nemaju jednoduche dokazy.
Pozri aj toto
http://mathworld.wolfram.com/PonceletsPorism.html
Inac v tejto knihe
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#46 29. 12. 2011 13:00 — Editoval vanok (29. 12. 2011 13:02)
Re: najkrajsia teorema
Dobry den,
Pridavam dalsiu peknu teoremu, pre ktoru mame vela dokazav:
JE to zakon kvadradickej reciprocity:
p, q su neparne prvocisla.
kde :
 je Legendrov symbol definovany takto
je Legendrov symbol definovany takto
cf.
http://cs.wikipedia.org/wiki/Legendre%C5%AFv_symbol
Pridavam odkaz na wikipediu
http://en.wikipedia.org/wiki/Quadratic_reciprocity
Ako aj referencie na niektore zo znamych dokazov
http://www.rzuser.uni-heidelberg.de/~hb3/rchrono.html
PACI SA VAM?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#48 29. 12. 2011 13:57
Re: najkrajsia teorema
↑ Matej1117:hovorí,že pre každé dvojicu prirodzených čísel n,t existuje prirodznené číslo p také,že platí
MATH IS THE BEST!!!
Offline
#50 07. 01. 2012 20:45
Re: najkrajsia teorema
Enigmaticka teorema:
Tu je url na google book
http://books.google.fr/books?id=87vciTx … mp;f=false
Si pozrite Theorem 2.4.8.
Ze je to krasna teorema!
A viete kto je jej autor?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


