Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Krivkovy integral II.druhu (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 12. 2011 16:15
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Krivkovy integral II.druhu
Nevite nekdo jak na to :
mam zadano:
integral_c y dx + x^(2) dy , kde c je cast paraboly: y= 4-x^(2) orientovana od bodu [2,0] do bodu [1,3]
jak dojdu k tomu ze,
x=3-t a y = 4-(3-t)^(2) a t nalezi <1,2>
nevite nekdo jak zjistim to x a proc zrovna je t <1,2> ??
diky
Offline
- (téma jako vyřešené označil(a) tigerhell22)
#2 10. 12. 2011 09:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Krivkovy integral II.druhu
Opět pozdrav,
x zparametrizuješ stejně jako tady - ze zadaných bodu vytvoříš směrový vektor přímky, na které je úsečka od bodu (2, 0) do (1, 3) - má být zajištěn i směr. A zapíšeš parametrické vyjádření x. Do y již dosazuješ vyjádření pro x. Hodnoty t opět najdeš z koncových bodů. Tedy x=3-t, musí z bodu (1) platit 2=3-t a také z bodu (2) platit 1=3-t.
Je to v pořádku? Děkuji.
Offline
#3 10. 12. 2011 11:01
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Re: Krivkovy integral II.druhu
↑ jelena:
Furt jsem nějak nepochopil jak dostat to x, to přeci nemůžu vyjadřit stejně jak u úsečky, pro parabolu to bude jinak ne ? to y chápu, to vycházi z toho x...
Offline
#4 10. 12. 2011 12:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Krivkovy integral II.druhu
↑ tigerhell22:
představ si, že pohyb po parabole sleduješ v čase (t) zároveň po ose x a po ose y. Po ose x je pohyb rovnoměrný (popisujeme lineárně), po ose y je závislost kvadratická. Srovnej s pohybem při šikmém vrhu, například.
Je to tak srozumitelné pro představu?
Offline
#5 10. 12. 2011 12:38
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Re: Krivkovy integral II.druhu
↑ jelena:
no tak trochu to srozumitelny je... ale jak jsi psala v tom prvním příspěvku, ž to udělam stejné jak u te usecky, tak by mi to vyslo takhle: x=(1-2)t+2 = 2-t ... ja jsem asi fakt dutej, ale prostě do toho nevidim... nemohla by jsi mi to rozepsat, jak se dostat presne k tomu x, z toho zadání..
děkuji..
Offline
#6 10. 12. 2011 15:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Krivkovy integral II.druhu
↑ tigerhell22:
tak to také může být (x=2-t), jen t bude v jiném intervalu (od 0 do 1 včetně), teď mne nenapadá žádný rozumný důvod, proč zrovna tak, jak to máte vy v řešení. Třeba někdo z kolegů doplní, děkuji.
Offline
#7 10. 12. 2011 16:26
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Re: Krivkovy integral II.druhu
↑ jelena:
dekuji, už mi to vychází, už jen poslední otazka, jak jsi poznala, že když je x=2-t , že ten interval bude od 0 do 1 ? a ne od 1 do 2 ...
Offline
#8 10. 12. 2011 16:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Krivkovy integral II.druhu
↑ tigerhell22:
sestavila jsem první část přímky v parametrickém tvaru (viz analytická geometrie SŠ)  . Abych měla úsečku omezím parametr t:
. Abych měla úsečku omezím parametr t: 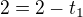 (pro 1. bod) a
(pro 1. bod) a 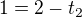 (pro druhý bod). Je to v pořádku? Děkuji.
(pro druhý bod). Je to v pořádku? Děkuji.
Offline
#9 10. 12. 2011 16:56
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Re: Krivkovy integral II.druhu
↑ jelena:
ok děkuji ti moc
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Krivkovy integral II.druhu (TOTO TÉMA JE VYŘEŠENÉ)