Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 12. 2011 14:26
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Průběh funkce
Zdravím všechny, chtěl bych Vás moc poprosit, nevím si rady s průběhem funkce: 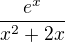
Definiční obor funkce jsem určitl jako R-{0,-2} A vypočtl jsem první derivaci která mi vyšla: 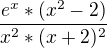 a druhou derivaci která vyšla:
a druhou derivaci která vyšla: 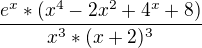
Dál už nevím jak z toho určit limity v nevlastních bodech, monotónost a extrémy. Zkoušel jsem i ostatní body jako konvexnost a konkávnost a a asymptoty, ale seděl jsem nad tím několik hodin a nepodařilo se mi to vyřešit. Toto zadání mi nějak nesedlo jiné zadání jsem vyřešil celkem v pohodě. že by to bylo tím 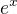 nevím.
nevím.
Děkuji předem všem kteří by mi s tímto chtěli pomoci.
Přejí pěkný předvánoční víkend.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 10. 12. 2011 17:28
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Průběh funkce
↑ Michaell0071:
Zdravím, přijde mi, že je špatně derivace:
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 10. 12. 2011 17:34 — Editoval standyk (10. 12. 2011 18:17)
Re: Průběh funkce
↑ Aquabellla:
Myslím, že tú prvú deriváciu má správne:
↑ Michaell0071:
Derivaciu polož nule a počítaj lokálne extrémy. Daná derivácia má 2 nulové body + z definičného oboru máme 2 body, v ktorých sa môže meniť monotónnosť. Číselnú os teda rozdelíme na 5 častí tými 4 bodmi a určujeme monotónnosť na jednotlivých intervaloch.
Druhá derivácia nemá nulové body takže stačí vyšetriť len v tých bodoch nespojitosti (ktoré nepatria do D(f)) či sa tam nemení z konkávnej na konvexnú, alebo naopak.
Asymptoty bez smernice počítaš ako limity v nevastných bodoch - ako si písal: Znamená to, že v tom bode má funkcia zvislú asymptotu. Podobne terba overiť aj limitu
Znamená to, že v tom bode má funkcia zvislú asymptotu. Podobne terba overiť aj limitu 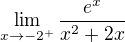
Asymptoty so smernicou počítaš ako: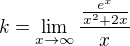 Ak je táto limita vlastná, tak daná funkcia má asymptotu so smernicou.
Ak je táto limita vlastná, tak daná funkcia má asymptotu so smernicou.
Offline
#4 10. 12. 2011 18:10
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk: Při počítaní lokálních extrémů si mám zvolit za x nějaké číslo z definičního oboru funkce? Děkuji :)
Offline
#5 10. 12. 2011 18:17 — Editoval cv (10. 12. 2011 18:18)
Re: Průběh funkce
↑ Michaell0071:
lokální extrémy a intervaly růstu a klesání:
urči, která čísla nulují první derivaci -> tedy pro která čísla je 1 derivace nulová.
Pomocí těchto čísel / bodů rozděl definiční obor na intervaly a urči, jestli je 1 derivace na jednotlivých intervalech klesající (záporná) nebo rostoucí(kladná)
Z toho už jednoduše určíš extrémy. pokud bude 1 derivace v levém okolí daného bodu záporná a v pravém okolí kladná, pak je v tom bodě minimum. obdobně s maximem. Ale bacha, extrém nastává jen v těch bodech, kde je funkce definovaná.
Potažmo tedy pokud ti vyjde "extrem" v bode, který sice nuluje první derivaci, ale není v definičním oboru funkce, tak se o extrém nejedná.
Offline
#6 10. 12. 2011 18:21 — Editoval standyk (10. 12. 2011 18:22)
Re: Průběh funkce
↑ Michaell0071:
Číselnú os rozdelíme nulovými bodmi z derivácie (v tých bodoch môže byť lokálny extrém). Keď ale vyšetrujeme monotónnosť musíme vyšetriť aj ako tie body nespojitosti ovplyvnili monotónnosť funkcie. Preto si číselnú os rozdelíme bodmi: 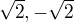 (nulové body derivácie)
(nulové body derivácie) (body nespojitosti - nepatria do definičného oboru.)
(body nespojitosti - nepatria do definičného oboru.)
Dosaď z jednotlivých intervalov nejaké x a zisti či na tom intervale je derivácia kladná alebo záporná.
Offline
#7 10. 12. 2011 19:26
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk: OK zkusím dosadit u obou intervalů. Uvidím co vyjde. Zatím díky moc.
Offline
#8 11. 12. 2011 10:43 — Editoval Michaell0071 (11. 12. 2011 10:43)
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
Ahoj, tak jsem dosadil do první derivace za  z intervalu od
z intervalu od  po
po 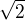 . A výsledk mi zde vyšel:
. A výsledk mi zde vyšel: 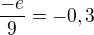 Pak jsem za
Pak jsem za  dosadil do první derivace z intervalu od
dosadil do první derivace z intervalu od 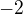 po
po  zde mě výsledek vyšel:
zde mě výsledek vyšel: 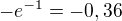
Počítal jsem i ty limity a ty mi vyšly: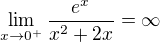


Je to co jsem vypíčítal k něčemu? Můžu to v tomto příkladu průběhu funkce nějak uplatnit?
Děkuji ještě jednou všem co se mi snaží pomoci. Ahoj
Offline
#9 11. 12. 2011 12:39 — Editoval standyk (11. 12. 2011 13:13)
Re: Průběh funkce
↑ Michaell0071:
Tie limity sú dobre, pretože keďže vyšlo že v bodoch nespojitosti (0,-2) má funkcia nevlastnú limitu. Znamená to, že v týchto bodoch má funkcia asymptoty bez smernice.
To že tá posledná limita je  tak môžeme povedať, že funkcia nemá asymptotu so smernicou.
tak môžeme povedať, že funkcia nemá asymptotu so smernicou.
Čo sa týka tej monotónnosti. Treba dosadiť čísla z každého podintervalu ktorý nám vznikol keĎ sme rozdelili tú číselnú os na 5 častí 4 bodmi. Čiže:
Na tých intervaloch kde je prvá derivácia záporná tam funkcia klesá a tam kde je derivácia kladná, tam rastie. Rovnako treba overiť aj v bodoch kde je derivácia rovná nula ( ) či je v týchto bodoch lokálny extrém
) či je v týchto bodoch lokálny extrém
Offline
#10 11. 12. 2011 22:08
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk: Tak jsem do první derivace z jednotlivých podintervalů a vyšlo mi:
pro 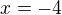 výsledek:
výsledek: 
pro  mi vyšlo:
mi vyšlo: 
pro 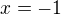 mi vyšel výsledk:
mi vyšel výsledk: 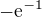
pro  mi vyšlo:
mi vyšlo: 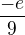
a pro  mi vyšlo:
mi vyšlo: 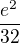
Pak jsem ještě dosadil do první derivace 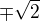 a zde jsem došel k výsledkům u obou
a zde jsem došel k výsledkům u obou 
Je to správně? Už je to všechno nebo je ještě třeba něco určit? Byly by jste tak hodní a dali mi to nějak dohromady aby jsem věděl co jsme to vlastně všechno vypočítali. Děkuji Vám mnohokrát. MOC děkuji standyk-ovi
Offline
#11 11. 12. 2011 23:16 — Editoval standyk (11. 12. 2011 23:20)
Re: Průběh funkce
↑ Michaell0071:
Čiže pre 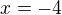 vyšlo číslo kladné, takže na intervale
vyšlo číslo kladné, takže na intervale 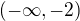 funkcia rastie.
funkcia rastie.
Pre  Ti vyšlo záporné - asi si sa pomýlil, lebo by malo vyjsť kladné- môžeš , takže na intervale
Ti vyšlo záporné - asi si sa pomýlil, lebo by malo vyjsť kladné- môžeš , takže na intervale  funkcia rastie.
funkcia rastie.
.....
V bodoch 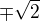 vyšlo 0. Treba sa teda pozrieť ako sa správa funkcia na jednotlivých intervaloch okolo týchto bodov.
vyšlo 0. Treba sa teda pozrieť ako sa správa funkcia na jednotlivých intervaloch okolo týchto bodov.
Vidíme (z prvej derivácie a z monotóonosti), že na intervale  funkcia rasie a na intervale
funkcia rasie a na intervale  funkcia klesa. Naľavo od bodu rastie a napravo klesá. Znamená to, že v bode
funkcia klesa. Naľavo od bodu rastie a napravo klesá. Znamená to, že v bode 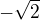 má funkcia lokálne maximum.
má funkcia lokálne maximum.
Podobne skús určiť aký extrém, a či vôbec má funkcia v druhom bode: 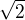
Jednotlivé kroky môžeš nájsť na napr. na stránke. Podľa toho si to už v pohode dáš dokopy - nie?
Offline
#12 11. 12. 2011 23:45
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
Jak určím zda je funkce sudá či lichá? Děkuji
Offline
#13 11. 12. 2011 23:50 — Editoval standyk (11. 12. 2011 23:54)
Re: Průběh funkce
↑ Michaell0071:
Musia byť splnené 2 podmienky. Párna (sudá)
A Nepárna (lichá):
Zadaná funkcia: 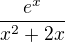 nesplňuje už tú prvú podmienku- konkrétne 2 leží v D(f) ale -2 neleží v D(f)
nesplňuje už tú prvú podmienku- konkrétne 2 leží v D(f) ale -2 neleží v D(f)
Inak, keby tá prvá podmienka bola splnená, tak by bolo treba overiť druhú podmienku: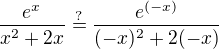 resp.
resp. 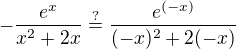
Offline
#14 12. 12. 2011 00:00 — Editoval Michaell0071 (12. 12. 2011 00:06)
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk:Takže tato funkce je lichá. ŽE ano?
Offline
#15 12. 12. 2011 00:02
Re: Průběh funkce
↑ Michaell0071:
NIE JE.
Už kôli tej prvej podmienke že 2 leži v D(f) ale -2 neleží v D(f) . A pozor na tie slová:
Funkcia, ktorá nie je lichá neznamená, že je sudá a naopak. Funkcia môže byť aj lichá aj sudá, alebo nemusí byť ani sudá ani lichá.
Offline
#16 12. 12. 2011 00:06
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk:intervalu 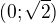 je funkce klesající a v intervalu
je funkce klesající a v intervalu  rostoucí že? JO takže funkce není asi sudá ani lichá není tomu tak.
rostoucí že? JO takže funkce není asi sudá ani lichá není tomu tak.
Děkuji Ti.
Offline
#17 12. 12. 2011 00:12
Re: Průběh funkce
↑ Michaell0071:
Áno správne. Čiže v bode 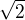 bude mať funkcia lokálne minimum.
bude mať funkcia lokálne minimum.
Áno, nie je ani párna ani nepárna (sudá lichá).
Pripájam aj graf
Offline
#18 12. 12. 2011 00:22 — Editoval Michaell0071 (12. 12. 2011 00:26)
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
Konvexnost a konkávnost na to se jde jak?? Mimochodem děkuji za graf. A inflexní bod funkce nemá?
Offline
#19 12. 12. 2011 00:31
Re: Průběh funkce
↑ Michaell0071:
Na to nám slúži tá druhá derivácia. Polož ju nule a počítaj nulové body. Zopakuj vlastne podobny proces ako pri prvej derivácii akurát namiesto monotónnosti budeš určovať konvexnosť, resp. konkávnosť, a v bodoch kde je druhá derivácia nulová môže byť ten inflexný bod.
Offline
#20 12. 12. 2011 00:37 — Editoval Michaell0071 (12. 12. 2011 10:19)
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk: Jak to mám udělat položit rovno nule, mám zas za  dosadit nějaké ty hodnoty jako u té monotónosti? Ne li uplně ty stejné. Díky za trpělivost.
dosadit nějaké ty hodnoty jako u té monotónosti? Ne li uplně ty stejné. Díky za trpělivost.
Offline
#21 12. 12. 2011 11:53
Re: Průběh funkce
↑ Michaell0071:
Treba dosadiť hodnoty, ktoré patria do tých jednotlivých intervalov (podobne ako pri prvej derivácii), ktoré Ti vzniknú, keď rozdelíš číselnú os tými nulovými bodmi z druhéj derivácie,
Offline
#22 12. 12. 2011 13:10
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk:Napsal bys mi prosím ty intervali z kterých mám dosadit do té druhé derivace. Díky moc
Offline
#24 12. 12. 2011 15:25
- Michaell0071

- Příspěvky: 105
- Reputace: 0
Re: Průběh funkce
↑ standyk:Nevím si s tím rady, které intervaly budou u té druhé derivace. Zkoušel jsem to a vyšly mi 
Offline
#25 12. 12. 2011 17:21
Re: Průběh funkce
↑ Michaell0071:
Nulové body sa získavajú z čitateľa, lebo keby bola v menovateli 0 tak by ten výraz nebol definovaný. V čitateli je súčin dvoch výrazov.  je kladné vždy a ten druhý výraz je tiež vždy kladný (môžeš to vidieť z grafu). To znamená že infelxné body tá funkcia nemá. Treba ale overiť na ktorých intervaloch je konvexná a na ktorých konkávna. Zase musíme použiť aj tie body nespojitosti (tak ako pri prvej derivácii). Preto rozdelíme číselnú os na 3 časti 2 bodmi (tie ktoré nepatria do D(f) = -2; 0) Dosadíme z jednotlivých intervalov čísla a zistíme, či je tam tá druhá derivácia kladná alebo záporná. Ak je kladná, tak funkcia bude na tom intervale konvexná a ak záporná tak bude konkávna.
je kladné vždy a ten druhý výraz je tiež vždy kladný (môžeš to vidieť z grafu). To znamená že infelxné body tá funkcia nemá. Treba ale overiť na ktorých intervaloch je konvexná a na ktorých konkávna. Zase musíme použiť aj tie body nespojitosti (tak ako pri prvej derivácii). Preto rozdelíme číselnú os na 3 časti 2 bodmi (tie ktoré nepatria do D(f) = -2; 0) Dosadíme z jednotlivých intervalov čísla a zistíme, či je tam tá druhá derivácia kladná alebo záporná. Ak je kladná, tak funkcia bude na tom intervale konvexná a ak záporná tak bude konkávna.
Offline
