Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Přepis postupu určitého integrálu (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 12. 2011 17:48
Přepis postupu určitého integrálu
Mám zadaný tento určitý integrál: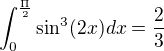
a tento textový popis jeho řešení:
Nejdriv substituci za 2x...\ 2x=b; 2dx=db; dx=1/2db \, pak prepocitas meze z 0->0 a pi/2->pi (dosad ty puvodni do ty substituce)
pak je teda integral .... 1/2 INT(z tech vypocitanejch mezi) (sin(b))^3 db
ted v tom integralu udelas fintu, ze si rozdelis ten sinus... sin*sin^2=sin*(1-cos^2)=sin-sin*cos^2
rozdelis to na dva integraly
1/2 INT(s mezema 0 a pi) sin b = 1/2[-cos x]0,pi = 1/2+1/2=1
ten druhej integral zase pres substituci....ted ale \ cos b=f; -sinb db=df \
zase prepocitas meze...pi->-1 , 0->1 a abychom si usetrili praci, vytknu ten minus od toho sin b, abych ho nemel v tom integralu, cims se mi z toho minulyho minusu udela plus
no a pak ted vyjde ten druhej integral +1/2 INT(od 1 do -1) f^2 df
coz jednoduse zintegrujes jako f^3/3
dosadis ty hodnoty do +1/2[f^3/3](od 1 do -1) .... a vyjde (+1/2)*(-1/3)-(1/2)*(1/3)=-2/6=-1/3
no a to odectes od ty 1 z prvniho integralu a vyjde 1-(1/3)=2/3
Mohl by jste mi to prosím někdo přepsat do nějaký lepší podoby? Díky :)) Mě nění jasný co je přepočet mezí.
SCIENTIA EST POTENTIA (Vědění je moc, ve znalostech je síla, vědění je síla)
Offline
- (téma jako vyřešené označil(a) -Jandy-)
#2 17. 12. 2011 20:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přepis postupu určitého integrálu
Zdravím,
-Jandy- napsal(a):
Mohl by jste mi to prosím někdo přepsat do nějaký lepší podoby?
všemi deseti?
a) mně není jasné a byste,
b) na přepis máme Editor LateXu - napravo od okna zprávy (na opravu "vypocitanejch", "minulyho" apod. máme odkazy na české slovníky)
c) přepočet mezí - pokud je  , v jakých mezích bude
, v jakých mezích bude 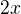 , což je substituováno jako
, což je substituováno jako  ?
?
Stačí tak? Děkuji.
Offline
#3 17. 12. 2011 22:49
Re: Přepis postupu určitého integrálu
jelena napsal(a):
Zdravím,
-Jandy- napsal(a):
Mohl by jste mi to prosím někdo přepsat do nějaký lepší podoby?
všemi deseti?
a) mně není jasné a byste,
b) na přepis máme Editor LateXu - napravo od okna zprávy (na opravu "vypocitanejch", "minulyho" apod. máme odkazy na české slovníky)
c) přepočet mezí - pokud je, v jakých mezích bude
, což je substituováno jako
?
Stačí tak? Děkuji.
Ahoj,
ono to je už spočítané, ale jenom v textové podobě a mě z toho není jasné co, kde, jak děje. Takže bych to potřeboval převést z této textové podoby do LaTexového editoru. Abych to viděl pořádně. Popřípadě přepočítat znovu :)
SCIENTIA EST POTENTIA (Vědění je moc, ve znalostech je síla, vědění je síla)
Offline
#4 17. 12. 2011 23:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přepis postupu určitého integrálu
-Jandy- napsal(a):
Takže bych to potřeboval převést z této textové podoby do LaTexového editoru. Abych to viděl pořádně. Popřípadě přepočítat znovu :)
:-) A jakou barvu rámečku bys přál?
Tady u kolegy - horní funkce bude 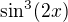 , dolní 0. Meze, jak máš zadáno, a nech počítat obsah množiny (1. čudlík). Potom v PDF klikneš na rámeček a projdeš s kolegou výpočet integrálu. Jednu změnu mezí jsem naznačila - podařilo se odpovědět na dotaz "V jakých mezích bude 2x?"
, dolní 0. Meze, jak máš zadáno, a nech počítat obsah množiny (1. čudlík). Potom v PDF klikneš na rámeček a projdeš s kolegou výpočet integrálu. Jednu změnu mezí jsem naznačila - podařilo se odpovědět na dotaz "V jakých mezích bude 2x?"
Druhou změnu mezí naznačíme až dojdeš ve výpočtu integrálu k potřebě měnit mez. Pro cvičení LaTeX máme pískoviště. Zdar přeji.
Offline
#5 17. 12. 2011 23:58 — Editoval Alivendes (18. 12. 2011 17:30)
Re: Přepis postupu určitého integrálu
Pokud smím, tak bych to řešil takto :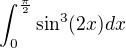
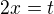

Přepočet mezí - Je dané že 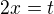
a)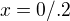


b)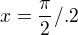
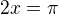
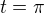
Pro mezi výpočet meze zanedbáme: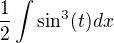
Využil bych této skutečnosti: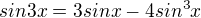
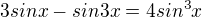
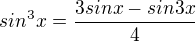
Dosadíme do našeho integrálu: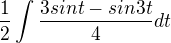
![kopírovat do textarea $\frac{1}{8} \[-3cost+\frac{cost}{3} \]$](/mathtex/f7/f77d478576d36a1fe6330e35c244c525.gif)
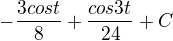
Dosadíme pro naší původní neznámou x:![kopírovat do textarea $\int_{0}^{\frac{\pi }{2}}\sin ^{3}(2x)dx = [-\frac{3cos2x}{8}]_{0}^{\frac{\pi }{2}}-[\frac{cos6x}{24}] _{0}^{\frac{\pi }{2}}=\[\([-\frac{3cos\pi}{8}]-[-\frac{3cos0}{8}] \)+\([\frac{cos\pi}{24}]-[\frac{cos0}{24}]\)\]= \nl \[\(\frac{3}{8}+\frac{3}{8}\)+\(-\frac{1}{24}-\frac{1}{24}\)\]= \frac{6}{8}-\frac{2}{24}=\frac{18-2}{24}=\frac{16}{24}=\frac{2}{3}$](/mathtex/a4/a41459814f6f7af63eeca9337780993a.gif)
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 18. 12. 2011 10:06
Re: Přepis postupu určitého integrálu
↑ -Jandy-:
Není za co :)
Záleží, jaký postup ti vyhovuje víc. Mně tohle přijde rychlejší než to, co jsi psal nahoře.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#8 18. 12. 2011 10:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přepis postupu určitého integrálu
↑ Alivendes:
Zdravím,
a) mně přijde rychlejší klasika pomocí  (kterou kolega v postupu má).
(kterou kolega v postupu má).
b) kolega potřeboval vysvětlit změnu mezí - toho se mu nedostalo (pravda, že může provést výpočet neurčitého integrálu "bokem" a potom dosadit původní meze, ale není to úplně správně - viz debata autorit). I jinak by mu nácvik změny mezí neuškodil.
c) poslala jsem kolegu, aby se obeznámil s online nástroje z úvodního tématu sekce VŠ, teď nevím, zda tam došel nebo ne.
d) pro zápisy goniometrických funkcí (a nejen) se má používat \ (zpětné lomítko), pokud šlo o přepis do LaTeX,
e) nabízením hotových řešení u kolegy vznikl dojem automatovosti naších odpovědí - věřím, že jsem mu to vyvrátila.
:-) samozřejmě velmi děkuji za ochotu a za Tvůj čas.
------------------
o tom, jak jsem milá a vstřícná, snad není třeba přesvědčovat - drobnost pro volné chvilky
Offline
#9 18. 12. 2011 11:07 — Editoval kaja.marik (18. 12. 2011 11:08)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Přepis postupu určitého integrálu
↑ Alivendes:![kopírovat do textarea $\frac{1}{8} \[-3cost+\frac{cost}{3} \]$](/mathtex/f7/f77d478576d36a1fe6330e35c244c525.gif)
nema byt ![kopírovat do textarea $\frac{1}{8} \[-3\cos t+\frac{\cos 3t}{3} \]$](/mathtex/7e/7ee1202a166f1986d517bfe7a894fe2e.gif) ?
?
pocitame ![kopírovat do textarea $\frac{1}{8}\[ \int3\sin tdt-\int \sin3tdt \]$](/mathtex/dd/ddb30a64d9052baf238a9e547892c8de.gif)
Offline
#10 18. 12. 2011 17:28 — Editoval Alivendes (18. 12. 2011 17:34)
Re: Přepis postupu určitého integrálu
↑ kaja.marik:
Vypadla mi trojka, ve finále to ale vychází stejně, proto jsem si nevšiml ...
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Přepis postupu určitého integrálu (TOTO TÉMA JE VYŘEŠENÉ)
