Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 01. 2012 15:43 — Editoval vanok (02. 01. 2012 16:30)
Re: Teorie čísel
Ahoj ↑ mipo:,
Ja vzdy najprv pozdravim, a ty...
a) Mozes skusis vyuzit ze 
b) zatial nemam inu myslienku ako
 a
a 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 02. 01. 2012 23:08 — Editoval vanok (02. 01. 2012 23:18)
Re: Teorie čísel
↑ mipo:,
a)
Z danej relacie mame

Skusme dosadzovat postupne prirodzene cisla take ze
 je positivne prirodzene cislo a nam da x positivne prirodzene.
je positivne prirodzene cislo a nam da x positivne prirodzene. nam da z
nam da z  ze
ze  , cize
, cize 
podobne
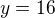 nam da
nam da  , cize
, cize 
 nam neda ziadne riesenie
nam neda ziadne rieseniePOKRACUJ
Dokaz ze toto nam da vsetki riesenia
a ze pre urcitu hodnotu
 metoda nam uz neda ziadne riesenie pre ziadne
metoda nam uz neda ziadne riesenie pre ziadne  take
take 
cize mozes po konecnom pocte hladani prestat hladat dalsie riesenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 03. 01. 2012 08:03
#6 03. 01. 2012 09:31
Re: Teorie čísel
Ahoj ↑ Honzc:,
Mozes dat url, kde sa najde ten tvoj software na kontrolu vysledkov.
Takto som mohol overit ze moja metoda co je vyssie je dokonala... co pochopopitelne je prijemne vediet.
Dakujem a Stastlivy Novy Rok 2012.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 03. 01. 2012 15:29
Re: Teorie čísel
Tady jsem napsal krátký program v wxMaxime, který vypíše čísla [x,y] pro které platí výše uvedené.
Také vypíše počet řešení.
Je velmi rychlý, neboť nezkouší čísla, která vyhovují, ale rovnou je vypíše.
Code:
fR(n):= block([x,y,L,p,q,k,S:[],T:[]],
L: divisors(n),
for p in L do (
for q in L do (
k: p/q,
if k>=1 then S: cons(k,S)
)
),
S: unique(sort(S)),
print("Počet řešení:",length(S)),
for k in S do (
x: n*(k+1),
y: n*(1/k+1),
T: cons([x,y],T)
), T
);Zkouška pro n=14:
fR(14);
Počet řešení: 5
[[210,15],[112,16],[63,18],[42,21],[28,28]]
Offline
#10 04. 01. 2012 13:02 — Editoval vanok (04. 01. 2012 13:04)
Re: Teorie čísel
↑ mipo:,
na ten druhy, poviem ti pravdu, nemal som casna to mysliet.
Jedina dobra novinka je mechanicka odpoved
http://www.wolframalpha.com/input/?i=3^ … or+n%3D105
Ktora nam dava, ze skutocne mame tu delitelnost.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 04. 01. 2012 13:59
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Teorie čísel
Zdravím,
k b) stačí ověřit, že
181/3^5 + 4^5
Offline
#12 04. 01. 2012 15:05
Re: Teorie čísel
Ahoj ↑ ruamaixanh:,
To som videl ze 181/3^5 + 4^5, ale preco to staci ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 05. 01. 2012 08:20 — Editoval Honzc (05. 01. 2012 08:50)
#14 05. 01. 2012 16:29
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Teorie čísel
↑ vanok:
Protože pro liché k platí:
Důvod: 
V našem případě 
Offline
#15 05. 01. 2012 17:07
Re: Teorie čísel
↑ ruamaixanh:
dakujem... niekedy cloveku ujdu jednoduchosti.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
 , ale tato co teraz navrhujem sa mi viac paci.
, ale tato co teraz navrhujem sa mi viac paci.
 pro
pro 
 pro
pro 



