Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferenciální rovnice 1. řádu s nekonstantnímy koeficienty (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 07. 2012 16:41
diferenciální rovnice 1. řádu s nekonstantnímy koeficienty
Dobrý den, prosím poraďte mi jak řešit tuto rovnici: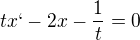
nedá se řešit pomocí charakteristické rovnice, na Wolframu mi to ukázalo nějaký postup ale tomu jsem moc neporozuměl.
Offline
- (téma jako vyřešené označil(a) Tuzex)
#5 07. 07. 2012 00:07
Re: diferenciální rovnice 1. řádu s nekonstantnímy koeficienty
↑ Tuzex:
Príkladom homogénnej rovnice je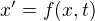
kde  je ľubovoľná funkcia, so splnenými príslušnými požiadavkami pre existenciu a jednoznačnosť riešenia x. Príkladom nehomogénnej rovnice je
je ľubovoľná funkcia, so splnenými príslušnými požiadavkami pre existenciu a jednoznačnosť riešenia x. Príkladom nehomogénnej rovnice je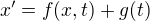
kde je vnesená nehomogenita prostredníctvom g. To je už časť rovnice, ktorá nezávisí od x, preto je rovnica nehomogénna. V našom prípade je tiež rovnica nehomogénna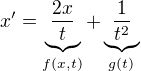
Postup pri riešení nehomogénnej rovnice je taký, že riešenie hľadáme v tvare
kde x_H je riešenie príslušnej homogénnej časti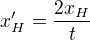
Tvar funkcie K sa nájde spätným dosadením ako je uvedené vo výpočte.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 07. 07. 2012 15:08
Re: diferenciální rovnice 1. řádu s nekonstantnímy koeficienty
↑ lukaszh:
děkuji za vysvětlení
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferenciální rovnice 1. řádu s nekonstantnímy koeficienty (TOTO TÉMA JE VYŘEŠENÉ)

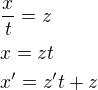
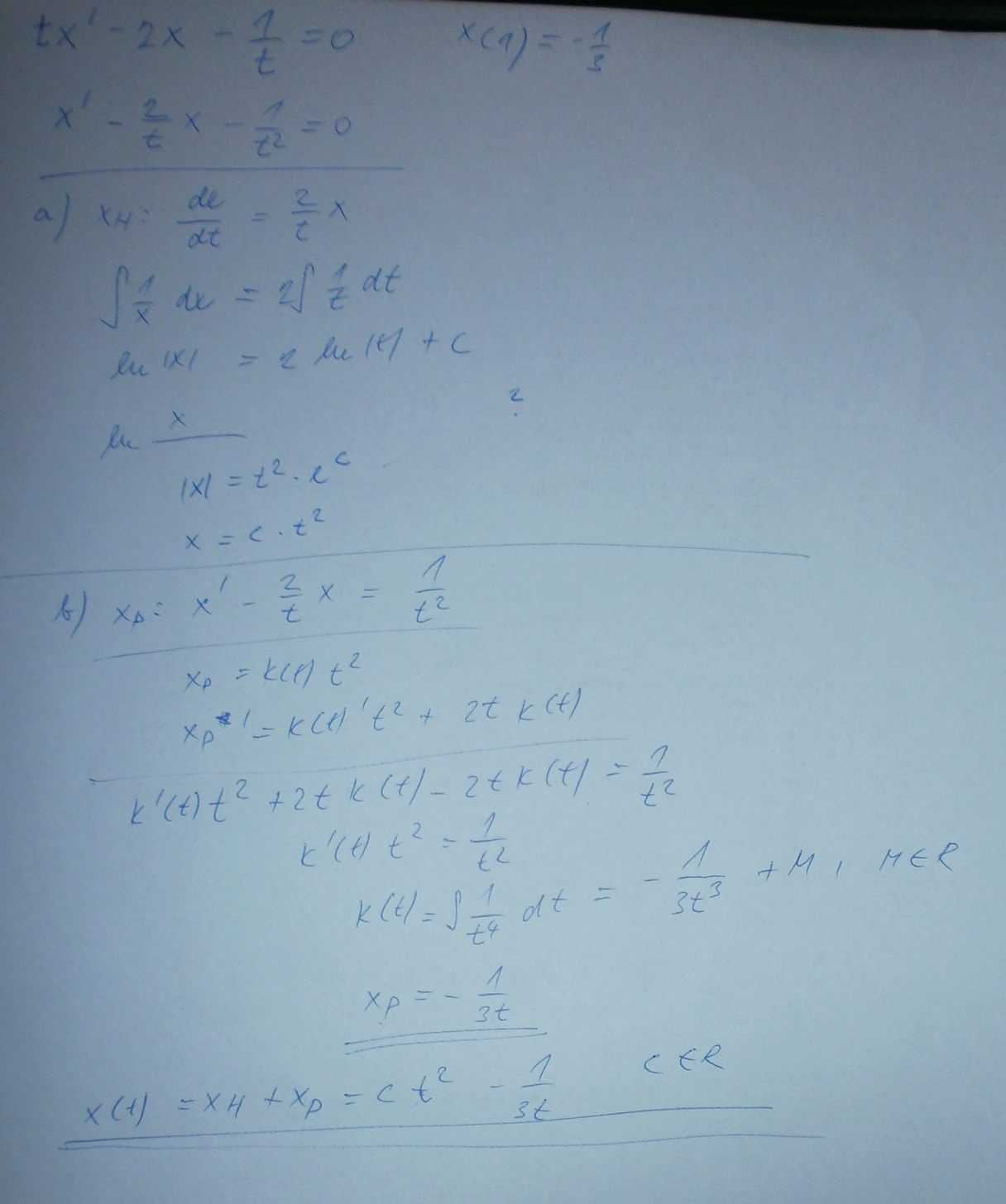
 ?
?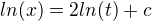
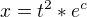 /nerozumim kde se vezme t na druhou
/nerozumim kde se vezme t na druhou