Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika a pravděpodobnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 03. 2011 11:52
Kombinatorika a pravděpodobnost
Ve skříni je rozházeno 6 různých párů střevíců. Večer potmě otec vybere 5 střevíců.
Jaká je pravděpodobnost,
a) že se z nich nechá sestavit alespoň jeden úplný pár?
b) že se z nich nedá sestavit ani jeden pár?
děkuji moc
Offline
- (téma jako vyřešené označil(a) jelena)
#2 09. 03. 2011 12:27 — Editoval musixx (09. 03. 2011 12:37)
Re: Kombinatorika a pravděpodobnost
↑ pavelek: Zdá se, že předpokládáme, že při vybírání není ani možno rozlišovat pravé a levé boty.
Takže z 12 bot jde 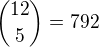 způsoby vybrat pět bot.
způsoby vybrat pět bot.
Pár nepůjde sestavit, vezmeme-li po jedné botě z různých párů. To se dá spočítat různě. Třeba vyberu jeden pár, ze kterého nevezmu žádnou botu (6 způsobů) a ze zbylých pěti párů vyberu nezávisle na sobě po jedné botě (2^5 způsobů). Nebo si boty na chvilku očísluji, vyberu z 12 bot jednu (12 způsobů), pak druhou botu z páru odstraním a vyberu zase jednu botu ze zbylých deseti, opět druhou do páru odstraním, vyberu další ze zbylých osmi, ... To celé pětkrát. No a na závěr se nebudu starat o to, jak bylo 5 vybraných bot setřízených, tedy v jakém pořadí jsem je bral (odtud ten "klasický" faktoriál ve jmenovateli). Samozřejmě dostanu stejný výsledek oběma metodama: 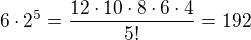 .
.
Stačí tak, že?
EDIT: Osobně bych lobboval za první přístup. Proč totiž v úloze, kde jde primárně o tzv. nerozlišitelné objekty, je prvně učinit rozlišitelnými a pak se té rozlišitelnosti "pracně" zbavovat? Umím si možná představit případy, kdy mi to možná víc pomůže než přidá práce, ale to zde není pravda.
Offline
#4 09. 03. 2011 12:38
#5 31. 10. 2011 19:24
Re: Kombinatorika a pravděpodobnost
A pak už je jen mezi sebou vydělím a mám výslednou pravděpodobnost, že??? Takže 24,24%??? A jak by to bylo, kdybych měl, že se z nich nedá sestavit ani jeden pár?
musixx napsal(a):
↑ pavelek: Zdá se, že předpokládáme, že při vybírání není ani možno rozlišovat pravé a levé boty.
Takže z 12 bot jdezpůsoby vybrat pět bot.
Pár nepůjde sestavit, vezmeme-li po jedné botě z různých párů. To se dá spočítat různě. Třeba vyberu jeden pár, ze kterého nevezmu žádnou botu (6 způsobů) a ze zbylých pěti párů vyberu nezávisle na sobě po jedné botě (2^5 způsobů). Nebo si boty na chvilku očísluji, vyberu z 12 bot jednu (12 způsobů), pak druhou botu z páru odstraním a vyberu zase jednu botu ze zbylých deseti, opět druhou do páru odstraním, vyberu další ze zbylých osmi, ... To celé pětkrát. No a na závěr se nebudu starat o to, jak bylo 5 vybraných bot setřízených, tedy v jakém pořadí jsem je bral (odtud ten "klasický" faktoriál ve jmenovateli). Samozřejmě dostanu stejný výsledek oběma metodama:.
Stačí tak, že?
EDIT: Osobně bych lobboval za první přístup. Proč totiž v úloze, kde jde primárně o tzv. nerozlišitelné objekty, je prvně učinit rozlišitelnými a pak se té rozlišitelnosti "pracně" zbavovat? Umím si možná představit případy, kdy mi to možná víc pomůže než přidá práce, ale to zde není pravda.
Offline
#6 01. 11. 2011 09:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika a pravděpodobnost
Pro kolegu chajdik
A pak už je jen mezi sebou vydělím a mám výslednou pravděpodobnost, že??? Takže 24,24%???
ano.
A jak by to bylo, kdybych měl, že se z nich nedá sestavit ani jeden pár?
Byl by to jev opačný k jevu "a) že se z nich nechá sestavit alespoň jeden úplný pár?"
-----------------------
Proč u vás na škole jsou tak tendenční úlohy? Např., proč cestuje žena, ale ne pasažér? Nebo co nutí ubohého otce vybírat boty potmě? o zkušených manželkách ani nemluvím, ale dobře jsem se bavila :-)
Zdravím v tématu a nejen.
Offline
#7 09. 10. 2012 20:19
- chelsea111

- Příspěvky: 48
- Reputace: 0
Re: Kombinatorika a pravděpodobnost
musixx napsal(a):
↑ pavelek: Zdá se, že předpokládáme, že při vybírání není ani možno rozlišovat pravé a levé boty.
Takže z 12 bot jdezpůsoby vybrat pět bot.
Pár nepůjde sestavit, vezmeme-li po jedné botě z různých párů. To se dá spočítat různě. Třeba vyberu jeden pár, ze kterého nevezmu žádnou botu (6 způsobů) a ze zbylých pěti párů vyberu nezávisle na sobě po jedné botě (2^5 způsobů). Nebo si boty na chvilku očísluji, vyberu z 12 bot jednu (12 způsobů), pak druhou botu z páru odstraním a vyberu zase jednu botu ze zbylých deseti, opět druhou do páru odstraním, vyberu další ze zbylých osmi, ... To celé pětkrát. No a na závěr se nebudu starat o to, jak bylo 5 vybraných bot setřízených, tedy v jakém pořadí jsem je bral (odtud ten "klasický" faktoriál ve jmenovateli). Samozřejmě dostanu stejný výsledek oběma metodama:.
Toto je výpočet, že nevybere ani jeden pár?
A jak by tedy bylo to, že vybere alespoň 1 pár?
Offline
#9 10. 10. 2012 09:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika a pravděpodobnost
Zdravím,
↑ musixx: děkuji.
↑ chelsea111:, ↑ Frankie11:
pokud dobře čtu téma, tak se vyřešila pravděpodobnost, že nevybere ani jeden (žádný) úplný pár.
a) že se z nich nechá sestavit alespoň jeden úplný pár?
Byl by to jev opačný ("též doplňkový či komplementární" (c)) k jevu "nevybere ani jeden úplný pár").
Offline
#11 10. 10. 2012 23:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika a pravděpodobnost
↑ Frankie11:
není za co, děkujeme kolegovi ↑ musixx:. Označím za vyřešené.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika a pravděpodobnost (TOTO TÉMA JE VYŘEŠENÉ)