Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 01. 2013 14:48
Homomorfismus
Ahoj, jelikož jsem marodil asi dva týdny a nebyl ve škole.Uniká mi jedná látka a to jsou homomorfismy, už jsem pochopil, jak určite jádro,obraz,ale pořád nevím, jak postupoval ,když je zadáno: Rozdhodněte,zda zobrazení  je homorfismus:
je homorfismus: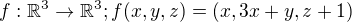 .Jak bych postupoval, k tomu, abych ověřil, zda jde o homomorfismus či nikoliv.
.Jak bych postupoval, k tomu, abych ověřil, zda jde o homomorfismus či nikoliv.
Offline
- (téma jako vyřešené označil(a) Kája2)
#3 04. 01. 2013 14:59
Re: Homomorfismus
↑ Mihulik:
Mám zde poznámku:
Zobrazení f do prostoru V do prostoru W se nazývá homomorfismus,jestliže pplatí:
1.)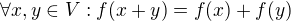
2.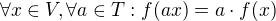 .
.
Ale nějak nevím, jak to kupříkladu na tento příklad použít
Offline
#5 04. 01. 2013 15:15 — Editoval Kája2 (04. 01. 2013 15:17)
Re: Homomorfismus
↑ Mihulik:
Trochu se v tom ztrácím....Mohu to chápat tak, že ji x+y =0, čili f(x+y)=f(o),pak f(x)+f(y) není rovno nule?
Offline
#6 04. 01. 2013 15:19 — Editoval Mihulik (04. 01. 2013 15:25)
Re: Homomorfismus
Zkus si rozmyslet, jestli může existovat lineární zobrazení  , pro které platí
, pro které platí 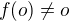 .
.
Odpověď:
Tím dostaneš odpověď na to, jestli tebou uvedené zobrazení
 je homomorfismus, či ne.
je homomorfismus, či ne. Offline
#7 04. 01. 2013 15:24 — Editoval Kája2 (04. 01. 2013 15:26)
Re: Homomorfismus
↑ Mihulik:
Aha,tak takhle.A budu tedy postupovat takhle stejně u dalších typů příkladů,že?Vlastně stále budu použit tento protipříklad.Chápu to dobře?
(Jinak mohl bych se ještě zeptat,jak bych to zapsal obecně na tomto příkladě přes ty zápisy f(x+y)=f(x)+f(y)?)
Offline

 nad tělesem
nad tělesem 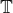 )
)  , kde
, kde  je nulový prvek tělesa
je nulový prvek tělesa 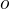 je nulový vektor vek. prostoru
je nulový vektor vek. prostoru 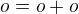 .
.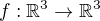 dáno předpisem
dáno předpisem 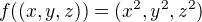 .
.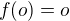 .
.