Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 02. 2013 20:40
Logaritmická nerovnice
Ahoj, já vím, že mi to bylo už jednou vysvětleno. Ale já prostě nevím... Mám tedy nerovnici
já si tedy udělám "kolotož a to že  a počítám to bez logaritmu a s jedničkou.
a počítám to bez logaritmu a s jedničkou.  následně se v tom ztrácím. Dělali jsme to a vcelku nedávno. Vím, že jsem to uměla, ale nemůžu to v tom sešitu prostě najít. Co s tím udělám teď?
následně se v tom ztrácím. Dělali jsme to a vcelku nedávno. Vím, že jsem to uměla, ale nemůžu to v tom sešitu prostě najít. Co s tím udělám teď?
Vím že si potom musím vypočítat ještě podmínku a to je že  vzniknou mi nulové body 3 a -3 a potom si nakreslím parabolu. Podle ní by měl být
vzniknou mi nulové body 3 a -3 a potom si nakreslím parabolu. Podle ní by měl být  . To zvládám. Mohl by mi to prosím někdo dovysvětlit?
. To zvládám. Mohl by mi to prosím někdo dovysvětlit?
Offline
- (téma jako vyřešené označil(a) jelena)
#2 15. 02. 2013 20:49 — Editoval Miky4 (15. 02. 2013 20:53) Příspěvek uživatele Miky4 byl skryt uživatelem Miky4. Důvod: Jsem nekňuba a plácám hlouposti.
#4 15. 02. 2013 20:59 — Editoval Freedy (15. 02. 2013 21:02)
Re: Logaritmická nerovnice
Ten váraz není definován na intervalu ![kopírovat do textarea $[-3;3]$](/mathtex/83/83f7632841f514b951b11167fe52e777.gif)
Když půjdeš od trojky do nekonečna tak budeš dostávat vždycky hodnoty z intervalu 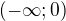
Když půjdeš od minus trojky do minus nekonečna tak budeš dostávat vždycky hodnoty z intervalu 
Takže výsledek dané nerovnice je že 
Miky4: nevím jak si přišel na to že 
Logaritmus o základu větším než jedna nabývá kladných hodnot když je výraz který logaritmuješ větší než jedna.
Takže toto platí
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 15. 02. 2013 21:01 — Editoval Miky4 (15. 02. 2013 21:03) Příspěvek uživatele Miky4 byl skryt uživatelem Miky4. Důvod: Jsem nekňuba a plácám hlouposti.
#6 15. 02. 2013 21:04 — Editoval Freedy (15. 02. 2013 21:05)
Re: Logaritmická nerovnice
ne miky4:
takhle:
http://www.wolframalpha.com/input/?i=lo … 9+%29%3E+0
PS: Základ logaritmu musí být vždy VĚTŠÍ než nula. Logaritmus nějakého čísla může být i záporný. Kolik asi myslíš že je dekadický logaritmus 1/10?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 15. 02. 2013 21:13
Re: Logaritmická nerovnice
grafem jsou dvě větve hyperboly. Můžeš to vidět na wolframu:
http://www.wolframalpha.com/input/?i=lo … 9+%29%3E+0
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#11 15. 02. 2013 22:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
Zdravím v tématu,
úkolem je vyřešit nerovnici  . Odlogaritmováním (základ je větší, než 1) dostáváme:
. Odlogaritmováním (základ je větší, než 1) dostáváme: , zároveň platí podmínka pro argument logaritmu:
, zároveň platí podmínka pro argument logaritmu: .
.
----------------------
Nerovnici  upravíme na anulovaný tvar:
upravíme na anulovaný tvar:

a tuto nerovnici řešíme. Výsledek ještě dáme do průniku s výsledkem nerovnice 
------------------------
vzniknou mi nulové body 3 a -3 a potom si nakreslím parabolu.
ano, v principu tento postup je použitelný - nerovnici v podílovém a v součinovém tvaru, která obsahuje jen "dvě závorky, ze kterých máme nulové body" - zde čitatel a jmenovatel můžeme řešit jako kvadratickou nerovnici - jen pozor, že v jmenovateli nesmí být 0 ani pro nerovnici s 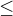
Jiný postup je tabulková metoda. Návrh zakreslovat hyperbolu 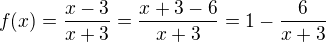 je také použitelný, ale zda se mi horší přehlednost v nalezení intervalů.
je také použitelný, ale zda se mi horší přehlednost v nalezení intervalů.
Kolega
Freedy napsal(a):
grafem jsou dvě větve hyperboly. Můžeš to vidět na wolframu:
http://www.wolframalpha.com/input/?i=lo … 9+%29%3E+0
nezakresluje hyperbolu, ale rovnou graf logaritmické funkce. Z toho je rozdíl. Mně vychází ![kopírovat do textarea $[-3;1]$](/mathtex/10/109c7bd4e72182a34b6e762ca6c202a3.gif) ,
,  pro pomocnou hyperbolu - graf lineární lomené funkce. Je tak? Děkuji.
pro pomocnou hyperbolu - graf lineární lomené funkce. Je tak? Děkuji.
Offline
#12 17. 02. 2013 21:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
↑ Anetka:
jelikož bylo nahlášeno, že pochopeno - děkuji, přidám ještě odkaz na Tvé stejné zadání.
Anetka napsal(a):
já vím, že mi to bylo už jednou vysvětleno.
a téma označím za vyřešené.
Offline


![kopírovat do textarea $[3;1]$](/mathtex/93/93671af2bfbdd719061b7877bfb5a3ae.gif) a
a 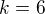 to by bylo posunuté trochu jinak nez to mate vy...
to by bylo posunuté trochu jinak nez to mate vy...