Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 03. 2013 18:22
Množiny
Mám příklad:
Do třídy chodí 28 žáků, kteří mohou chodit do tří kroužků (označených písmeny A, B, C). Do kroužku A chodí 14, do B 12 a do C 10 žáků, 6 žáků nechodí do žádnýho kroužku. Do všech kroužků zároven chodí 4 žáci. a mám vypočítat počet žáků, kteří navšetěvují právě 2 kroužky.
Udělal jsem si takový ty vennovy diagramy, a označil si to a - h, ale došel jsem jen k tomu že vím h to jest ti co nechodí nikam, a e to jsou ti co chodí do všech tří zároven. Ale nevím co s tím.
Byla by nějaká rada? Díky
Offline
- (téma jako vyřešené označil(a) Domki)
#3 04. 03. 2013 19:09 — Editoval Domki (04. 03. 2013 19:28)
Re: Množiny
no když použiju tento diagram: http://www.inflow.cz/files/redakce/VennuvDiagram.jpg
a rozepíšu to tak dostanu několik rovnic: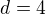

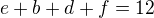

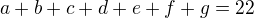 (28-6)
(28-6)
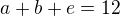
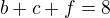

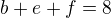
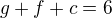
Ato když chcu ty co chodí prave do 2 by melo byt e+g+f = ?
Ale ted nevím jak dál
Offline
#9 04. 03. 2013 20:33 — Editoval ((:-)) (05. 03. 2013 11:36)
Re: Množiny
Offline
