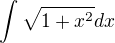Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 04. 2013 21:29 — Editoval martisek (05. 04. 2013 21:29)
Re: -
↑ paha154:
To je myslím z bláta do louže. Podle mě by bylo jednodušší vzít
a integrovat per partes. Nad gonometrickou substitucí zkusím zapřemýšlet
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#8 06. 04. 2013 20:09
#9 06. 04. 2013 22:44 — Editoval paha154 (17. 04. 2013 10:48) Příspěvek uživatele paha154 byl skryt uživatelem paha154.
#10 17. 04. 2013 10:53 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#11 17. 04. 2013 12:27
Offline
#12 17. 04. 2013 13:57 Příspěvek uživatele paha154 byl skryt uživatelem paha154.
#13 17. 04. 2013 17:18
#14 17. 04. 2013 21:41 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#15 18. 04. 2013 10:45
Re: -
↑ paha154: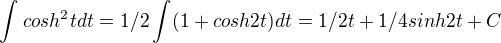
nebo tady http://cs.wikibooks.org/wiki/Integrov%C … %AD_metoda
přímo z definice hyperbolického cosinu.
Pokud se tedy nemýlím.
Offline
#16 18. 04. 2013 11:19 — Editoval paha154 (18. 04. 2013 15:45) Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#17 18. 04. 2013 18:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
↑ paha154:
Zdravím,
hned na úvod bych použila úpravu: , potom je substituce>
, potom je substituce>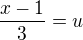 a dál už pokračovat dle doporučení kolegů (s
a dál už pokračovat dle doporučení kolegů (s  ).
).
K tomu integrálu máme velmi podrobně téma ve zlatém fondu.
Offline

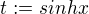 , protoze
, protoze 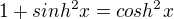 ...
...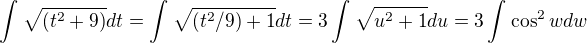 a zbytek už by měl být v pohodě.
a zbytek už by měl být v pohodě.