Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 04. 2013 22:19
Offline
#3 22. 04. 2013 22:30 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#4 22. 04. 2013 23:42
Re: -
Jj napsal(a):
↑ paha154:
Není v zadání integrálu nějaký překlep?
panebože, :( to vážně matika potřebuje příklady na míru, aby je dokázala spočítat? :'-(
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 23. 04. 2013 10:41 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#8 23. 04. 2013 12:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
↑ paha154:
děkuji za upřesnění - ale z toho, co vidím ve výsledku WA, to moc zajímavě nevypadá - kolega ↑ Freedy: bude zklamán. Trošku jsem včera zkoušela upravovat goniometrické vzorce, zkus také použit "poslední šanci" goniometrických substitucí.
Nebyl zadán jako určitý? Zdroj - Praha nebo Liberec? Děkuji.
Offline
#9 23. 04. 2013 13:50 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#10 23. 04. 2013 15:08 — Editoval martisek (23. 04. 2013 15:09)
Re: -
↑ Freedy:
Mílý Freedy,
neber jméno Boží nadarmo. Matematika, stejně jako fyzika, chemie či jakýkolv jiný obor lidské činnosti, jenom prostě není všemocná. Představ si chemika, který má za úkol vyrobit zlato, a dostane
1. Zlatou naplaveninu a vodu.
Zlato vyrobí.
2. Kovový sulfid, vodu a olej
Zlato vyrobí.
3. Pyrit, chlorové vápno, kyselinu sírovou a vodu.
Zlato vyrobí.
4. Vodu a kouř z doutníku.
Chemik řekne - sorry, Freedy, to nejde. A ty vykřikneš: Panebože, to ta chemie vážně potřebuje suroviny na míru, aby dokázala vyrobit zlato? Možná se budeš divit, ale potřebuje...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#11 23. 04. 2013 21:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
↑ paha154:
ne, v tomto původním zadání bych spíš ověřovala, zda to tak skutečně bylo myšleno - to je problém si ověřit u autora zadání? Případně - pokud je ze sbírky - jak vypadá zadání před a po tomto integrálu? Výsledek asi není k dispozici (že bychom se pokusili najít chybu v zadání i od výsledku) - tak?
Ten druhý integrál jsem myslela  , zkusila jsem ho ještě upravit goniometrickými vzorci a použit substituci
, zkusila jsem ho ještě upravit goniometrickými vzorci a použit substituci 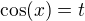 , potom výsledek nevypadá nejhůř, ale pořád se mi zdá nějaký nevzhledný k integrování (nepoužila jsem absolutní hodnotu, když jsem odmocňovala sinus z výrazu pod odmocninou - jen pro zběžný náhled).
, potom výsledek nevypadá nejhůř, ale pořád se mi zdá nějaký nevzhledný k integrování (nepoužila jsem absolutní hodnotu, když jsem odmocňovala sinus z výrazu pod odmocninou - jen pro zběžný náhled).
martisek napsal(a):
4. Vodu a kouř z doutníku.
bude velmi záležet na kvalitě vody :-)
Offline
#12 25. 04. 2013 16:25 Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Omylem vloženo dříve, než byl příspěvek dokončen
#13 25. 04. 2013 17:01 — Editoval Jj (25. 04. 2013 17:06)
Re: -
↑ paha154:
Tedy k tomu "druhému" integrálu:
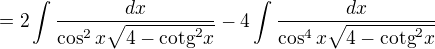
Nyní substituce:
tgx = t
dx/cos^2x = dt
cos^2x = 1/(t^2+1), po substituci integrály sloučit. Dostaneme integrál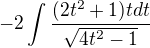 , ten po další substituci
, ten po další substituci
4t^2 - 1 = z
tdt = dz/8
2t^2 + 1 = (z + 3)/2 přímo zintegrovat.
Pokud se tedy nemýlím.
Offline
#14 25. 04. 2013 21:46 — Editoval jelena (26. 04. 2013 07:33)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
kolega Jj napsal(a):
Děkuji, k takovému zápisu jsem také došla použitím goniometrických vzorců - ↑ v příspěvku 11: jsem tento upravený výraz vložila do WA, ale závěr jsem neviděla - děkuji za dovršení.
EDIT: tak nemám stejnou úpravu, ještě tu svoji projdu.
Offline
#15 01. 05. 2013 14:57 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#16 01. 05. 2013 23:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
↑ paha154:
Děkuji za zprávu.
To mi nešlo, tak jestli jim tam opravdu vypadlo to x
:-) to se snad dá u nich zeptat (co je zdroj zadání?). Děkuji.
Offline
#17 02. 05. 2013 09:06 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#18 02. 05. 2013 09:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
↑ paha154:
:-) to já "náhodou" narazím tak akorát na nezaplacenou složenku a ještě přesně vím, odkud pochází.
Děkuji za poskytnuté upřesnění.
Offline

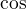 měl za argument výraz
měl za argument výraz ![kopírovat do textarea $\sqrt[4]{4-\text{cotg}^{2}x}$](/mathtex/6e/6eb339c3dbc01b3540d0b970d1756cc4.gif) . Přesně - dosud nikdy :-) Kolega Ji. asi také - je tak, kolego? Děkuji.
. Přesně - dosud nikdy :-) Kolega Ji. asi také - je tak, kolego? Děkuji.