Matematické Fórum

Firejs · 29. 04. 2013 21:46

Ahojte,

mám tu jeden příklad, prošel jsem učebnici a žádný podobný jsem bohužel nenašel.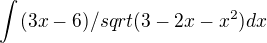
$\int_{}^{} (3x-6)/sqrt(3-2x-x^2)dx$

Kdy to bylo takto: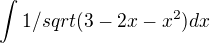
$\int_{}^{} 1/sqrt(3-2x-x^2)dx$
Tak to upravím na: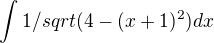
$\int_{}^{} 1/sqrt(4-(x+1)^2)dx$
A dopočítám dle vzorce...

Ale ta vrchní část mi tam přebývá, tak mě napadlo mě, že by se to mělo dát řešit přes rozklad, jenže tam by zase neměla být odmocnina... jaký postup zvolit? Díky.

Fido · 29. 04. 2013 22:04 — Editoval Fido (29. 04. 2013 22:15)

Dvojitá substituce. Dole si to nejdříve doplnit na čtverec. Potom si zvolit substituci t=x+1 - zbavíš se závorky a nahoře si vytkneš trojku, kterou dáš před integrál. Po těhle krocích ti zbyde 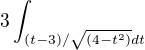$3\int_{(t-3)/\sqrt{(4-t^2)} dt}^{}$ a zde zvolíš substituci t=2sin(q), tudíž dt=2cos(q). Spodek se ti vykrátí a zbyde ti 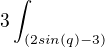$3\int_{(2sin(q)-3)}^{}$ což už v pohodě zintegruješ a povracíš substituci. Nejtěžší je na tomhle najít si tam ty goniometrický funkce, ale to chce cvik a vidíš je v tom schovaný.

Firejs · 29. 04. 2013 22:32

Díky, to už jen na mě trochu "silné kafe", ale zkusím na to přijít.

Fido · 29. 04. 2013 22:49

↑ Firejs: Ono obecně žij s tím, že odmocniny (pokud pod nima není šikovný na druhou, takže ti zmizí, nebo se to nedá přepsat jako x na něco - je tam mnohočlen) se dost blbě integrujou, takže to skoro vždycky vede na substituci. A pak je dobrý v různejch zlomkách vidět právě ty goniometrický funkce, protože ti to většinou krásně usnadní.

010010 · 29. 04. 2013 23:09

Môj postup: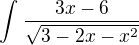
$\int_{}^{}\frac{3x-6}{\sqrt{3-2x-x^2}}$
polynóm 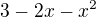$3-2x-x^2$ má reálne korene 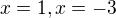$x=1 , x=-3$ a $a<0$
máme teda 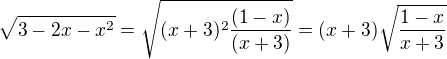$\sqrt{3-2x-x^2}=\sqrt{(x+3)^2 \frac{(1-x)}{(x+3)}}= (x+3)\sqrt{\frac{1-x}{x+3}}$
po dosadení: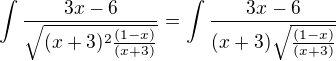
$\int_{}^{}\frac{3x-6}{\sqrt{(x+3)^2 \frac{(1-x)}{(x+3)}}}= \int_{}^{}\frac{3x-6}{(x+3)\sqrt{\frac{(1-x)}{(x+3)}}}$
Substitúcia: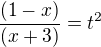 $\frac{(1-x)}{(x+3)}=t^2$ dostáveme 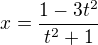$x= \frac{1-3t^2}{t^2+1}$ takže
$dx=\frac{-8t}{(t^2+1)^2}dt$

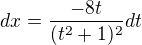
Ak som dobre dosadil, tak nám to vypľuje: 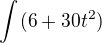$\int_{}^{}(6+30t^2)$ (brať s rezervou).
Každopádne pomocou substitúcie ktorú som použil, som si to upravil na krajší tvar.

jelena · 29. 04. 2013 23:25 — Editoval jelena (30. 04. 2013 00:04)

Zdravím,

doplním ještě postup úpravy integrovaného výrazu, aby v čitateli se našla derivace jmenovatele atd. Snad se také použije. A tuším - Mendelu by v tomto případě využilo i Ostrogradského metodu - viz odkazované téma a MAW.

EDIT: přehozeno čitatele/jmenovatele

Matematické Fórum

#1 29. 04. 2013 21:46

Integrál polynomu s odmocninou ve zlomku

#2 29. 04. 2013 22:04 — Editoval Fido (29. 04. 2013 22:15)

Re: Integrál polynomu s odmocninou ve zlomku

#3 29. 04. 2013 22:32

Re: Integrál polynomu s odmocninou ve zlomku

#4 29. 04. 2013 22:49

Re: Integrál polynomu s odmocninou ve zlomku

#5 29. 04. 2013 23:09

Re: Integrál polynomu s odmocninou ve zlomku

#6 29. 04. 2013 23:25 — Editoval jelena (30. 04. 2013 00:04)

Re: Integrál polynomu s odmocninou ve zlomku

Zápatí