Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Teorie množin - výzkum jedné "množiny"
#1 11. 07. 2013 13:48
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Teorie množin - výzkum jedné "množiny"
Ahoj,
lze prostředky teorie množin (např. ZFC) ukázat, že existuje množina  s vlastností
s vlastností 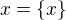 ? Nebo obecněji (speciálněji): lze prostředky teorie množin ukázat, že existuje množina
? Nebo obecněji (speciálněji): lze prostředky teorie množin ukázat, že existuje množina  s vlastností
s vlastností 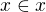 ?
?
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#3 11. 07. 2013 14:36 — Editoval Pavel Brožek (11. 07. 2013 14:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Teorie množin - výzkum jedné "množiny"
Ahoj, já myslím, že naopak lze ukázat, že taková množina neexistuje. Předpokládejme, že existuje množina  taková, že
taková, že  . Podle axiomu dvojice je
. Podle axiomu dvojice je 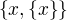 množina a je jistě neprázdná (obsahuje
množina a je jistě neprázdná (obsahuje  ). Podle axiomu fundovanosti
). Podle axiomu fundovanosti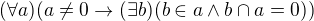
tedy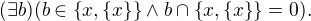
Množina 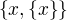 má maximálně dva různé prvky
má maximálně dva různé prvky  a
a 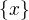 . Pokud
. Pokud 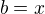 , pak
, pak 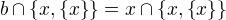 . Ale
. Ale  patří jak do
patří jak do  tak do
tak do 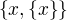 , patří tedy i do průniku a průnik je tak neprázdná množina. Kdyby
, patří tedy i do průniku a průnik je tak neprázdná množina. Kdyby  , tak
, tak 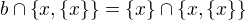 . A opět,
. A opět,  patří do obou množin v průniku, takže je průnik neprázdná množina. To je spor s axiomem fundovanosti.
patří do obou množin v průniku, takže je průnik neprázdná množina. To je spor s axiomem fundovanosti.
Edit: Na wikipedii se o tom také píše.
Offline
#4 11. 07. 2013 20:26
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Teorie množin - výzkum jedné "množiny"
↑ Pavel Brožek:
Děkuji. Podobně by nejspíš bylo možné dokázat i to, že neexistuje "řetězec"  , apod.
, apod.
"Máte úhel beta." "No to nemám."
Offline
#5 11. 07. 2013 22:02
Re: Teorie množin - výzkum jedné "množiny"
Pozdravujem.
Pozri sa na NF ( new fundations), uvidis ze tvoj vzorec ma v nej zmysel.
Pozor, ide o teoriu mnozin, co sa chova inac ako ZF.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Teorie množin - výzkum jedné "množiny"