Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Neurčitý integrál, substituce, per partes, nevychází (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 11. 2013 18:43
Neurčitý integrál, substituce, per partes, nevychází
Zdravím, mám takový problém. Už jsem tento příklad počítal snad 5x, ale stále se nemůžu dopracovat k výsledku, který by byl stejný jako výsledek z WolframAlpha. Tady odkaz pro porovnání, červenou barvou je výsledek integrace od WA, modře je výsledek mé integrace.
Kde mám chybu? Co jsem přehlédl?
Offline
- (téma jako vyřešené označil(a) jelena)
#2 27. 11. 2013 18:53
Re: Neurčitý integrál, substituce, per partes, nevychází
↑ Thomas123:
Dobrý večer, jestli dobře chápu výsledek Wolframu, pak se výsledky liší jen o konstantu.
To pak znamená, že jsou oba výpočty v pořádku.
Pokud se tedy nemýlím.
Offline
#3 27. 11. 2013 19:00
Re: Neurčitý integrál, substituce, per partes, nevychází
Dobrý večer, děkuji za odpověď.
Pokud by se ale výsledky lišily pouze o konstantu, tak by obě vykreslené fce byly stejné (spojité), ale pouze posunuté vůči sobě po ose Y, což dle vykreslení Wolframem není - můj výsledek vykreslený je spojitý, zatímco výsledek integrace Wolframu je nespojitý. Chápu to správně? Nicméně nyní jsem zkusil integraci programem MAW na mendelu.cz a mají stejný výsledek jako já. Je tedy možné, že můj výsledek je správný, ale zadal jsem to špatně do Wolframu, příp. Wolfram vyhodil špatný výsledek?
Offline
#4 27. 11. 2013 19:40
Re: Neurčitý integrál, substituce, per partes, nevychází
↑ Thomas123:
Řekl bych, že v tom případě bude rozumnější, pokud se k věci vyjádří někdo ze znalejších kolegů. Na to si netroufám.
Pokud se tedy nemýlím.
Offline
#5 27. 11. 2013 21:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál, substituce, per partes, nevychází
Zdravím,
kolega Jj napsal(a):
Řekl bych, že v tom případě bude rozumnější, pokud se k věci vyjádří někdo ze znalejších kolegů.
:-) pokusím se tomu vytvořit podmínky a přesunout na správný stůl a také poprosím o vyjádření.
Pokud se dívám na úplně 1. člen v WA (... -4), tak mám dojem, že musel při úpravách něco podnikat s převodem arctg(2/(x+2)) za využití arccotg - a to je WA potíž.
↑ Thomas123: největší jistoty získáš zderivováním svého výsledku a porovnáním se zadáním. V každém případě v 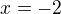 funkce není definována (ale zřejmě jen vypíchnutý bod - museli bychom došetřit zleva a zprava).
funkce není definována (ale zřejmě jen vypíchnutý bod - museli bychom došetřit zleva a zprava).
Offline
#6 27. 11. 2013 21:45 — Editoval kaja.marik (27. 11. 2013 21:54)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Neurčitý integrál, substituce, per partes, nevychází
Souhlasim s Jelenou, potiz je v tom bode nespojitosti. Jinak na kazdem intervalu neobsahujicim bod x=-2 to vypada, ze se lisi o konstantu, takze vse je v poradku.
Primitivni funkce je definovana na otevrenem intervalu a je vzdy spojita. Nekdy je nutne ji dolepit se spojitych kousku, jak treba u http://forum.matweb.cz/viewtopic.php?id=67165
Offline
#7 28. 11. 2013 12:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál, substituce, per partes, nevychází
↑ kaja.marik:
Zdravím Vás a děkuji,
ještě jsem uvážila, že obejit takovou nepěknost,jako člen z úpravy na začátku (x^2+4x-4) a 6 před posledním členem (všechno je nečekané ohledem na původní zadání funkce), rovnou použit ve WA substituci x+2=t a tak zapsat. Zvláštní, že nespojitá 0 mu nevadí :-)
Pravděpodobně bude fungovat i u jiných problému s nespojitosti (obvykle se na to ani nedíváme při neurčitých integrálech), zde snad podobná situace.
Offline
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Neurčitý integrál, substituce, per partes, nevychází (TOTO TÉMA JE VYŘEŠENÉ)
