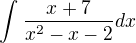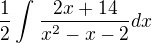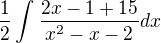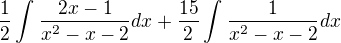Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 12. 2013 21:23
- om2kvv@gmail.com

- Příspěvky: 40
- Reputace: 0
ako volit postup na výpocet integralu
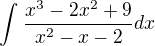
počítal som tento integrel, keď som si ho rozdelil na parcialne zlomky tak mi zostalo 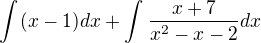
a tu vzniká problém, keď si menovatel rozložíme na 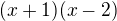 tak vychádza iný výsledok ako keď si v čitateli upravíme na deriváciu menovatela a použijeme vzorec kde podiel derivácie funkcie/funkcia=ln(funkcia)
tak vychádza iný výsledok ako keď si v čitateli upravíme na deriváciu menovatela a použijeme vzorec kde podiel derivácie funkcie/funkcia=ln(funkcia)
Ktorý postup je správny a prečo? Veľmi ďakujem za pomoc!
Offline
#2 15. 12. 2013 21:51
Re: ako volit postup na výpocet integralu
oba postupy su spravne a vyjdu rovnake vysledky, len to s tou derivaciou je podla mna zbytocna komplikacia, lebo ten rozklad na parcialne zlomky tam potom aj tak robis.
tu mas spravny vysledok
http://www.wolframalpha.com/input/?i=in … -x-2%29+dx
ak ti to vychadza inak tak napis postup a chybu najdeme
Offline
#4 15. 12. 2013 22:43 — Editoval greenic (15. 12. 2013 22:45)
Re: ako volit postup na výpocet integralu
↑ om2kvv@gmail.com:
Ten druhy integral ve vysledku je spatne ne? prece 1 neni derivaci x2-x
Offline
#5 15. 12. 2013 23:02 — Editoval om2kvv@gmail.com (15. 12. 2013 23:03)
- om2kvv@gmail.com

- Příspěvky: 40
- Reputace: 0
Re: ako volit postup na výpocet integralu
teraz som si uvedomil že ten vzorec co som chcel aplikovať na ten druhý(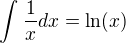 ), by sa asi nedal tak som to chcel skusit cez arctg,
), by sa asi nedal tak som to chcel skusit cez arctg, 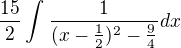
ale arctg, vo vylsedku neni :(
uz fakt neviem co kedy mozem pouzit, HELP pls.
Offline
#6 15. 12. 2013 23:08
#7 15. 12. 2013 23:59 — Editoval Brano (16. 12. 2013 00:00)
Re: ako volit postup na výpocet integralu
↑ om2kvv@gmail.com:
to je prave to co som hovoril, ze tak ci tak by si tam potom musel robit rozklad na parcialne zlomky t.j.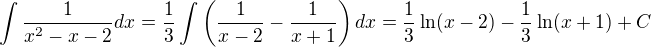
cize je jednoduchsie ho robit hned v integrali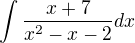
Offline
#8 16. 12. 2013 05:52
- om2kvv@gmail.com

- Příspěvky: 40
- Reputace: 0
Re: ako volit postup na výpocet integralu
↑ Brano:
Ďakujem,
A ako mam pri pocitani vedieť ze arctg sa neda na to pouzit, lebo ako som napisal sedi mi to aj na ten vzorec
Offline
#9 16. 12. 2013 10:30
Re: ako volit postup na výpocet integralu
↑ om2kvv@gmail.com:
Řekl bych, že pro užití arctg by ten integrál musel mít ve jmenovateli znaméko +: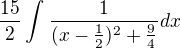
Pokud se tedy nemýlím.
Offline