Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - nalezení chyby (TOTO TÉMA JE VYŘEŠENÉ)
#3 02. 01. 2014 22:05
Re: Integrál - nalezení chyby
↑ Arabela:
Možná dělám něco špatně, ale vyšlo mi to samé
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#6 02. 01. 2014 22:44
Re: Integrál - nalezení chyby
↑ Arabela:
Děkuji, jen by mě zajímalo, proč nefunguje substituce. Když se postupuje matematicky správně.
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#7 02. 01. 2014 22:51
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrál - nalezení chyby
Meglun napsal(a):
↑ Arabela:
Děkuji, jen by mě zajímalo, proč nefunguje substituce. Když se postupuje matematicky správně.
Alek kdepak, nein to spravne. Je to mismas, od integralu funkce jedne promenne x prejdete k integralu se dvema promennymi (x a t), potom se sin(x) vytahne ven jako kdyby to byla konstanta, ale ona to konstanta neni. Proste to je hokej s pisemnky podle podivnych pravidel.
Offline
#8 02. 01. 2014 23:24
Re: Integrál - nalezení chyby
Ahoj ↑ Meglun:,
čo sa týka metódy substitúcie, tá sa hodí iba niekedy... Po dosadení premennej za substituovaný výraz a za diferenciál novej premennej sa už "stará" premenná v substituovanom výraze nesmie nachádzať. Pokiaľ hrozí, že sa zvolenou substitúciou nezbavíme "starej" premennej, substitúcia nie je "namieste". Kolega kaja.marik má pravdu, keď Ti to vytkol...
server.gphmi.sk/~domanyov
Offline
#9 03. 01. 2014 00:11
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrál - nalezení chyby
Čistě pro budoucí generace: pokud chci v integrálu  substituci
substituci 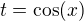 tak můžu psát třeba
tak můžu psát třeba  a
a  . Po dossazení
. Po dossazení  a vidím, že jsem si integrál spíš zkomplikoval.
a vidím, že jsem si integrál spíš zkomplikoval.
Offline
#10 03. 01. 2014 13:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál - nalezení chyby
Zdravím v tématu,
↑ kaja.marik:
pokud budoucí generace nařídí, že bude substituce za goniometrickou funkci, tak můžeme rozšířit  a po rozdělení na 2 zlomky nějakou tu substituci najdeme - co bychom pro generace neudělali :-)
a po rozdělení na 2 zlomky nějakou tu substituci najdeme - co bychom pro generace neudělali :-)
↑ Meglun:
ověřuješ své kroky pomocí online nástrojů úvodního tématu? Děkuji
Offline
#13 03. 01. 2014 16:17
Re: Integrál - nalezení chyby
↑ Arabela:
Děkuji, této úpravy jsem si nevšiml
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - nalezení chyby (TOTO TÉMA JE VYŘEŠENÉ)





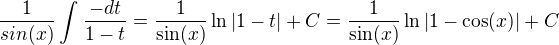


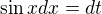

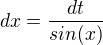

 ,
, .
.
