Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Subdirektně irreducibilní algebra (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 01. 2014 13:32 — Editoval Andrejka3 (07. 01. 2014 21:12)
Subdirektně irreducibilní algebra
Ahoj,
mám tu jednu větu, která charakterizuje subdirektně ireducibilní algebry.
Značení: značme  nejmenší kongruenci algebry a
nejmenší kongruenci algebry a  největší.
největší.
Věta 2: Nechť je  algebra. Pak
algebra. Pak je subdirektně ireducibilní, právě když je triviální, nebo
je subdirektně ireducibilní, právě když je triviální, nebo  (tj. právě když
(tj. právě když 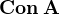 obsahuje právě jeden atom).
obsahuje právě jeden atom).
Můj problém: neumím dokázat implikaci 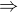 .
.
Mám k dispozici tuhle větu:
Věta 1: Algebra  je izomorfní subdirektnímu součinu algeber
je izomorfní subdirektnímu součinu algeber  , právě když existují
, právě když existují 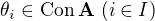 tak, že platí
tak, že platí 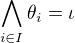 .
.
V tomto případě lze položit  .
.
Díky za pomoc.
Edit: Věta 2 je následně použita k důkazu Birkhoffovy věty.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 07. 01. 2014 20:42 — Editoval OiBobik (07. 01. 2014 22:46)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Subdirektně irreducibilní algebra
↑ Andrejka3:
(Ty se snad učíš na tutéž zkoušku, jako teď já... : D )
1) Tam má být  , ne?
, ne?
2) Nechť tedy je  SD-irr. algebra, která není triviální (což nevím, co znamená, ale tak budu předpokládat, že to implikuje
SD-irr. algebra, která není triviální (což nevím, co znamená, ale tak budu předpokládat, že to implikuje  ). Uvažujme pro libovolnou sadu kongruencí na
). Uvažujme pro libovolnou sadu kongruencí na 
 homomorfismus
homomorfismus  daný jako
daný jako ![kopírovat do textarea $a \mapsto ([a]_{\alpha_i})_{i\in I}$](/mathtex/c6/c636b2b66bdb595bb20ebff167516352.gif) . Pak
. Pak  je prostý, právě když
je prostý, právě když 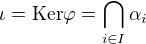 .
.
Nyní kdyby 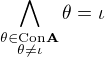 ,
,
je takové  určené sadou všech oněch netriviálních kongruencí SD vnoření (a tedy
určené sadou všech oněch netriviálních kongruencí SD vnoření (a tedy  SD rozklad
SD rozklad  ) Přitom pro žádné
) Přitom pro žádné  není
není  isomorfismus, jelikož jeho jádro je
isomorfismus, jelikož jeho jádro je  . Tedy
. Tedy  nebyla subdirektně ireducibilní.
nebyla subdirektně ireducibilní.
Podobně se dá vykoukat i druhá implikace (za pomoci 1. věty o isomorfismu).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 07. 01. 2014 21:11 — Editoval Andrejka3 (07. 01. 2014 21:17)
Re: Subdirektně irreducibilní algebra
↑ OiBobik:
Ahoj :)
1) Jo, máš pravdu, opravím to.
2) Ano, triviální algebru mi definovali jako jednoprvkovou. Takže tak.
Díky, moc krásná odpověď. Ještě to úplně nechápu, ale myslím, že mi to dojde, až nad tím pořádně popřemýšlím.
edit:
OiBobik napsal(a):
↑ Andrejka3:
Přitom pro žádnénení
isomorfismus, jelikož jeho jádro je
. Tedy
nebyla subdirektně ireducibilní.
Podobně se dá vykoukat i druhá implikace (za pomoci 1. věty o isomorfismu).
Uvidím, zda mi to zvýrazněné neudělá potíž. Včera mě děsilo tohleto: http://forum.matweb.cz/viewtopic.php?id=69015
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 07. 01. 2014 21:28 — Editoval OiBobik (07. 01. 2014 21:29)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Subdirektně irreducibilní algebra
↑ Andrejka3:
To se tváří záhadně, ale je to jenom ten fakt, že člověk ví, jak ta složenína vypadá, a sice jako ![kopírovat do textarea $a \mapsto [a]_\theta$](/mathtex/96/960c3bb34070e527ec4d4167b448c0fa.gif) . Takhle když se to napíše, tak je to celkem jasný. : ))
. Takhle když se to napíše, tak je to celkem jasný. : ))
Ale máš pravdu, souvisí to spolu: všimni si, že v definici SD-irr algebry není, že je při každém svém SD-rozkladu isomorfní některému z těch součinitelů, ale že ta konkrétní složenína pro některý ten součinitel je isomorfismus.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 07. 01. 2014 21:35
Re: Subdirektně irreducibilní algebra
Jo, došlo mi to původní. Super! Bohužel, zítra už mám zk, takže toho už moc nestihnu. Díky a hodně štěstí na Tvé zk.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 07. 01. 2014 21:53 — Editoval Andrejka3 (07. 01. 2014 21:54)
Re: Subdirektně irreducibilní algebra
↑ OiBobik:
Takže definice z mých skript je špatně, že? SD-irr, právě když: je-li
SD-irr, právě když: je-li  izomorfni SD algeber
izomorfni SD algeber 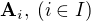 , pak existuje
, pak existuje 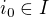 tak, ze
tak, ze 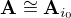 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 07. 01. 2014 22:05 — Editoval OiBobik (07. 01. 2014 23:24)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Subdirektně irreducibilní algebra
↑ Andrejka3:
Nevím, jestli špatně.
Já to znám jinak a podporujíe to například tato učebnice (strana cca 57).
Myslím, že to ve výsledku je jedno, ale tady se hodí ta "moje definice": Když se ukáže Birkhoffova věta (tj. o rozkladu do nějaké množiny SD-irr algeber) pro tu "moji definici", tak pak SD irr algebra "podle tvé definice" bude mít SD irr rozklad, kde ty komponenty budou SD irr "podle mé definice". Pak podle tvé definice je jedné z nich ta uvažovaná SD irr algebra isomorfní, což ve výsledku znamená, že musí být taky SD irr "podle mé definice", neboť ta je invariantní vůči isomorfismu (jako asi jakákoli kategoriální definice...)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 07. 01. 2014 22:17
Re: Subdirektně irreducibilní algebra
↑ OiBobik:
Děkuju.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Subdirektně irreducibilní algebra (TOTO TÉMA JE VYŘEŠENÉ)