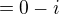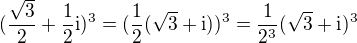Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2014 22:05 — Editoval bonifax (15. 04. 2014 22:10)
komplexní čísla
Ahoj, chtěl poprosit o pomoc, jak pokračovat v tomto postupu? Po umocnění na druhou mi zbyly dva členy, takže jsem se posunul jen o kousek nepatrně /.)
Předem díky.
dodatek: Pomocí převodu na gonio. tvar to mám již vyřešené, tak bych rád tento postup.
Řešte bez kalkulačky!
Reálná část komplexního čísla 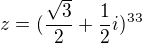 je rovna
je rovna
a) 1 b) -1 c) 0 d) 
![kopírovat do textarea $(\frac{\sqrt{3}}{2}+\frac{1}{2}i)^{33}=[(\frac{\sqrt{3}}{2}+\frac{1}{2}i)^2]^{15}*(\frac{\sqrt{3}}{2}+\frac{1}{2}i)^{3}=$](/mathtex/e5/e539e3290f74881c15766cb2306baf7f.gif)
![kopírovat do textarea $[\frac{3}{4}+\frac{2\sqrt{3}i}{4}+\frac{1}{4}i^2]^{15}*(\frac{\sqrt{3}}{2}+\frac{1}{2}i)^{3}=[\frac{1}{2}+\frac{\sqrt{3}i}{2}]^{15}*(\frac{\sqrt{3}}{2}+\frac{1}{2}i)^{3}$](/mathtex/ea/ea0e9e071d621cd2b89659b7b32d05b3.gif)
Offline
- (téma jako vyřešené označil(a) bonifax)
#2 15. 04. 2014 22:13
Re: komplexní čísla
Ahoj ↑ bonifax:,
Ako prve vyjadri z v goniometrickom zapise ( cize z cos a sin)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 15. 04. 2014 22:31
Re: komplexní čísla
Tvoj postup je priliz dlhy aby si prisiez k vysledku v rozumnom case.
Metoda co som ti navrhol, ak ovladas tvoje vzorce je maximum 5 minut prace!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 15. 04. 2014 22:47 — Editoval bonifax (15. 04. 2014 22:49)
Re: komplexní čísla
↑ vanok:
tento postup jsem již použil a šlo to v pohodě. Je to postup, který používá zdenek1 na svým webu:
http://materialy.rubesz.cz/prijimaci_zkousky/vse-11-a0/
- PRIKLAD Č. 14.
Většinou po umocnění na druhou zbyl pouze jeden člen s imaginární složkou, takže to šlo vpohodě pak dořešit.
Co se týká převodu, tak to není problém, ale chtěl bych znát tento postup, který mám již rozpočítaný.
Offline
#6 15. 04. 2014 22:59 — Editoval Freedy (15. 04. 2014 23:19)
Re: komplexní čísla
Ahoj,
to co zde na fóru občas předvádí zdeněk ale funguje pouze za předpokladu že a = b.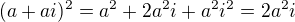
není to žádný univerzální postup, pouze elegantní. Zde navíc ani nemáš sudý exponent, takže je to zbytečně zdlouhavé dělat to přes čtverec, lepší je použít krychli:
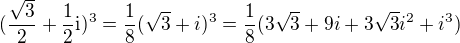
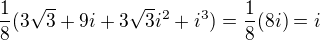

L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 15. 04. 2014 23:23 — Editoval vanok (15. 04. 2014 23:26)
Re: komplexní čísla
↑ bonifax:,casto existuje viac metod.
Ako vidim, tu co som ti navrhol podla casu tvojho a mojho prispevku ti trvalo 16 min. to je trocha vela. Ale iste to dokazes zlepsit.
Vyhoda metody cis je ze ju mozes pouzit prakticky vzdy.
Tiez je to metoda co ti da okamzitu odpoved, ak by si chcel za kazdu cenu pracovat na algebrickej forme, ako to urobit co najekonomicky...
Akoze na kolegovu metodu mas dokumentaciu, tak ju mozes kludne pouzit.
Poznamka: ↑ bonifax: v tvojom vypocte si mohol najprv zjednodusit zlomok 33/6, a tiez pouzit périodu 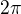
A na koniec nemas ani konecny vysledok na danu otazku.odpoved je -1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 15. 04. 2014 23:27
Re: komplexní čísla
vanok napsal(a):
Vyhoda metody cis je ze ju mozes pouzit prakticky vzdy.
To jistě ano, ale algebraická metoda zahrnuje daleko víc možností řešení, než goniometrická. Pokud se teda bavíme o počítání bez kalkulačky.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#11 15. 04. 2014 23:41 — Editoval vanok (15. 04. 2014 23:46)
Re: komplexní čísla
↑ Freedy:,
To iste zavisi od ludi. Na cis, tiez nebolo treba pouzit nic ine ako zname vedomosti. A rychlost dvoch metod si sam porovnaj.
Ozaj tato mnemotechnika ti hovori nieco?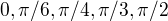

zabavne a pre niehoho aj uzitocne! ( poznal si to)
Co sa tyka pocitania, bez kalkulacky, kde maju vyst pekne hodnoty sa pouzivaju skoro vzdy ( na strednej skole) len uhly ktorych ( alebo ich "nasobku") sin a cos sa da jednoducho vyjadrit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 15. 04. 2014 23:44 — Editoval bonifax (15. 04. 2014 23:45)
Re: komplexní čísla
↑ Freedy:
jj aha jasny už :D , díky
↑ vanok:
vánku :D, já ale nesleduji nepřetržitě jenom tohle forum, proto nemůžu reagovat hned na každou odpověď. Chtěl jsem znát tenhle konkrétní postup, nikoli přes převod na gonio. tvar, který jsi mi navrhoval ty. To jsem uvedl i při založení topiku ;-)
Ten příklad jsem, ale nepočítal, mám ho již vyřešený, takže jsem ho jen přepisoval do texu. Výsledek je mi zřejmý z posl. tvaru, který jsem uvedl, určitě i tobě, tak nač uvádět výsledek.
i tak díky za odpovědi , Měj se.)
Offline
#13 15. 04. 2014 23:47
Re: komplexní čísla
↑ bonifax:,
Ok, latex to nas brzdi, ze.
Tak dobre pokracovanie a vela uspechov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 16. 04. 2014 07:18
Re: komplexní čísla
vanok:
samozřejmě si myslím že goniometrický tvar je na umocňování k.č. nejlepší (stejně tak exponenciální).
Mě šlo jen o to, že kdyby jsi měl například: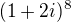 tak už by se to goniometricky z hlavy řešit nedalo, ale algebraicky pořád ano.
tak už by se to goniometricky z hlavy řešit nedalo, ale algebraicky pořád ano.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#15 16. 04. 2014 11:01
Re: komplexní čísla
Ahoj ↑ Freedy:
To mas pravdu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline