Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2014 09:28
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Průběh funkce
Zdravím,
potřebovala bych pomoct dořešit průběh funkce, došla jsem k druhé derivaci, ale bohužel si nevím rady, jak mám pokračovat dál. Dále mám určit ještě: Lokální minimum, Lokální maximum, Inflexní body, Funkce konvexní x konkávní, Limity v nevlastních bodech – limity pro nekonečno, limity to pro mínus nekonečno, Limity v bodech nespojitosti-
Mohla bys vás požádat o pomoct? Předem moc děkuji.
Funkce je následující:
Offline
#2 20. 04. 2014 11:03
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Průběh funkce
↑ Světoběžník:
Tak to vem popořadě, lokální extrémy určíš pomocí první derivace, zkus teda navrhnout jaký postup by jsi zvolil:)
Offline
#3 20. 04. 2014 13:27
Re: Průběh funkce
najskôr to podel tí x na 2 aby to nebolo take zamotane potom poderivuj a poloz rovne nule malo by to byt : 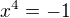
ak pracujes v R tak nema maximum ak v C tak extrem je v 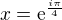 a zderivovat druhý raz pre stúpajúcu alebo klesajúcu a tak dalej :)
a zderivovat druhý raz pre stúpajúcu alebo klesajúcu a tak dalej :)
↑ Světoběžník:
Offline
#4 20. 04. 2014 16:30
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
Tkaže, první derivaci mám dát rovno nule, vypočítat ji jako normální rovnici, a to co mi z toho vyjde, tak bude co? minimum, maximum? ↑ Crashatorr:
Offline
#5 20. 04. 2014 16:41
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
Když jsem to vypočítala tak mi vyšlo x1= 0, x2= -1,3, x3= 0,78, ale vůbec nevím co s tím a ani si nejsem jistá, že to mám dobře.. :)↑ Světoběžník:
Offline
#6 20. 04. 2014 16:57 Příspěvek uživatele Světoběžník byl skryt uživatelem Světoběžník.
#7 20. 04. 2014 17:10
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
Pokusila jsem to se vypočítát sama, mohla byste mi to prosím celé zkontrolovat, jestli to mám celé dobře? Předem děkuji. :)
1. D(f)= R 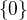
2. Průsečíky s osami:
s osou x: [1;0], [-1;0], s osou y: neexistujou
3. Body nespojitosti: x=0
4. Funkce je sudá
5. První derivace: -2(x^4+1)/ x^3
6. Stacionární body: nejsou
7. fce rostoucí: (0; )
)
8. fce klesající: (-  ;0)
;0)
9. Druhá derivace: -2(x^4-3) /x^4
10. Lokální minimum x maximum: to nevím, vyšly mi 3 kořeny : x1=0, x2=-1,3, x3= 0,78
11. inflexní body: 1,19
12. fce konvexní: (-  ; 1,19)
; 1,19)
13. fce konkávní: (1,19; )
)
14. Limity v nevlastních bodech: 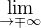 = 1
= 1
15. Limity v bodech nespojitosti:  = 1
= 1
To by mělo být vše, ale nejsem si tím vůbec jistá, tak jestli byste mi to mohl prosím zkontrolovat, potřebuju to mít dobře. Předem děkuji :)
Offline
#8 21. 04. 2014 01:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
Zdravím, zkus, prosím, co jde překontrolovat v online nástrojích (MAW jsi zkoušela?), potom se ještě ozvi, pokud najdeš nějakou nesrovnalost nebo nejasnost.
Hodnoty 1,19 není dobré tak zapisovat. Pokud vyšlo něco jako ![kopírovat do textarea $\sqrt[4]{3}$](/mathtex/57/57c6826f8d68ebeb2eb9c503d3a515e2.gif) (jen příklad zápisu), tak to tak nech i v řešení.
(jen příklad zápisu), tak to tak nech i v řešení.
10. Lokální minimum x maximum: to nevím, vyšly mi 3 kořeny : x1=0, x2=-1,3, x3= 0,78
To se mi nezdá - napsala jsi, že stacionární body nejsou (máme pouze bod x=0, kde derivace není definována). Odkud tedy 3 kořeny? Naopak inflexních bodů by mělo být více.
14. a 15. limity - mám úplně jinak, jak jsi postupovala? Zkus ještě projít přes nástroje. Děkuji.
Offline
#9 21. 04. 2014 09:37
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
Inflexní body jsou teda x1=−3,25, x2=3,25 ( mám to ve zlomku, jen nevím jak se to tady píše)
tím pádem fce konvexní (-  ; -3,25)
; -3,25)
fce konkávní (3,25;  )
)
mám to dobře?
a limity v nevlastních bodech nejsou žádné.
a v bodech nespojistosti mi teda vyšla 1. dosadila jsem do původní fce 0 protože bod nespojitosti je 0. tak nevím.
a když teda nejsou žádné stacionární body, ják mám určit ty lokální extrémy? děkuji
↑ jelena:
Offline
#10 21. 04. 2014 10:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
↑ Světoběžník:
Děkuji, překontrolovala jsi všechno, co šlo, pomocí MAW a WA? Např. pokud 2. derivace je tak, jak máš:
-2(x^4-3) /x^4
potom body podezřelé z inflexe jsou řešením rovnice 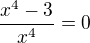 . Ovšem nesmíš zapomínat, že změna konvexní/konkávní může proběhnout i přechodem přes bod x=0 (který sice není v def. oboru, ale nesmíme na něho zapomenout, také je to nulový bod pro stanovení znamének 1. a 2. derivace).
. Ovšem nesmíš zapomínat, že změna konvexní/konkávní může proběhnout i přechodem přes bod x=0 (který sice není v def. oboru, ale nesmíme na něho zapomenout, také je to nulový bod pro stanovení znamének 1. a 2. derivace).
tím pádem fce konvexní (-
; -3,25)
fce konkávní (3,25;)
mám to dobře?
toto nebude dobře, jelikož chybí intervaly až do 0 a od 0.
a limity v nevlastních bodech nejsou žádné.
a v bodech nespojistosti mi teda vyšla 1. dosadila jsem do původní fce 0 protože bod nespojitosti je 0. tak nevím.
to není dobře. Nejde říci, že "nejsou žádné", pokud máš na mysli limity k +/- nekonečnu, tak to musíš došetřit (např. l´Hospitalem). Limitu k x=0 nemůžeš počítat dosazováním, ale vyšetřením zleva a zprava k 0.
Pokud stacionární body nejsou, tak vyšetřuješ jen znaménko derivace pro určení rostoucí/klesající. Zde však máme bod x=0, který není v def. oboru ani funkce, ani derivace, přechodem přes tento bod také dochází ke změně znaménka 1. derivace. Zatím máš rostoucí/klesající nedobře.
Zkus, prosím, maximálně, co jde, zkontrolovat v MAW a ve WA a vložit sem odkazy s komentářem. Máš bohužel v postupu dost zmatku (předpokládám, že samotný podrobný postup máš).
Zlomek se zapisuje tak \frac{čitatel}{jmenovatel} napravo od okna zprávy máš Editor TeX. Potřebuji však odejít za nějaký čas do práce, tak spíš k večeru se podívám. Případně si založ samostatné téma na dílčí dotazy - např. jen na limity, ať pomůže někdo z kolegů (kolegům děkuji). Měj se.
Offline
#11 21. 04. 2014 14:28
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
http://um.mendelu.cz/maw-html/index.php … orm=prubeh tady posílám ten odkaz, tohle mi vypočítalo.
↑ jelena:
Offline
#12 21. 04. 2014 14:33
- Světoběžník
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Průběh funkce
DObrý den, potřebovala bych pomoc určit lokální extrémy, fce konvexní, konkávní, a limity v bodech nespojitosti z funkce  , zkoušela jsem to už několikrát a pořád mi to nevychází. Už jsem pořádně zoufalá. Tady posílám i odkaz pro lepší dořešení.
, zkoušela jsem to už několikrát a pořád mi to nevychází. Už jsem pořádně zoufalá. Tady posílám i odkaz pro lepší dořešení.
http://um.mendelu.cz/maw-html/index.php … orm=prubeh
Moc prosím o pomoc, řeším to už celý víkend, zítra to potřebuju odezvdat a pořád to mám špatně... :( Děkuji!!!
Offline
#13 21. 04. 2014 16:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
↑ Světoběžník:
děkuji, v historii MAW jsem vložení viděla - z toho jsi něco vybrala do průběhu? Z MAW máš před sebou i graf, ke kterému se máš dopracovat.
Potom všechno můžeš krokově vložit do WA, jen si to musíš správně použit. Např. najdu body podezřelé z inflexe, najdu na kterém intervalu je 2. derivace kladná (tedy funkce je konvexní).
Příklad limity k +nekonečnu.
Pokud potřebuješ podrobný postup např. na limity, tak si, prosím, založ samostatné téma jen pro limitu.
Offline
#14 21. 04. 2014 17:45
#15 21. 04. 2014 19:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
↑ Světoběžník:
WAP (jako MAW) napsal exponent v podobě zlomku 3^(1/4), tedy ![kopírovat do textarea $3^{\frac{1}{4}}=\sqrt[4]{3}$](/mathtex/67/673e6289343a4c565ba0436a689f43ca.gif) , což je totéž. Zkus možná v MAW zvolit možnost výstupu v pdf, zda nebude lépe vidět.
, což je totéž. Zkus možná v MAW zvolit možnost výstupu v pdf, zda nebude lépe vidět.
Offline
