Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Operátor divergence (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 05. 2014 21:21
Operátor divergence
Ahoj, mohl by mi někdo poradit? Mám vektor r=x*i+y*j+z*k, kde i, j , k jsou jednotkové vektory, má spočítat divergenci výrazu div((r*c)*r) =? , kde c je konstanta (konstantní vektor), ví někdo, co s tím? Já jsem dospěl k výsledku 2*c*r, ale dle několika nezávislých zdrojů je správný výsledek 4*c*r.
Díky Lukáš.
Offline
- (téma jako vyřešené označil(a) Mr.Luc)
#3 26. 05. 2014 09:15 — Editoval Mr.Luc (26. 05. 2014 09:16)
Re: Operátor divergence
r je polohový vektor o souřadnicích x,y,z, jehož divergence je konkrétně 3. Nicméně divergence toho výrazu mi vychází jinak, než jsem našel v několika nezávislých zdrojích: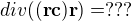 . Má to vyjít
. Má to vyjít 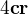 , já jsem došel k výsledku při výpočtu podle definici
, já jsem došel k výsledku při výpočtu podle definici  , ale nevím, kde bych mohl udělat chybu, možná neumím derivovat:)
, ale nevím, kde bych mohl udělat chybu, možná neumím derivovat:)
Lukáš.
Offline
#9 26. 05. 2014 10:19
Re: Operátor divergence
↑ Rumburak:
Čili doporučuješ použít vztah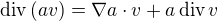 pro
pro  vektorovou,
vektorovou,  skalární funkci, chápu-li správně.
skalární funkci, chápu-li správně.
Offline
#12 26. 05. 2014 10:46 — Editoval Bati (26. 05. 2014 10:47)
Re: Operátor divergence
↑ Rumburak:
No v podstatě jsi ten vzorec odvodil, protože, když ponechám označení 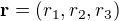 , tak jsi napsal
, tak jsi napsal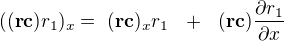
a vysčítáním, jak jsi naznačil, dostaneme rovnost  .
.
Mně se ten vzorec dobře pamatuje, protože je to stejné schéma jako právě derivace součinu 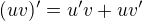 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Operátor divergence (TOTO TÉMA JE VYŘEŠENÉ)

 , kde
, kde 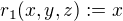 ,
, 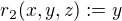 ,
,  . Teď už mi to sedí na divergenci, protože je to závislý na 3 proměnných, předtím jsem to nechápal, nejsem fyzik :-)
. Teď už mi to sedí na divergenci, protože je to závislý na 3 proměnných, předtím jsem to nechápal, nejsem fyzik :-) .
. ,
,  ) např.
) např.  ,
,  .
.  jak píšu, jinak by to ani nesedělo dimenzema. Divergence musí být z vektoru. Skalární součiny značím výhradně
jak píšu, jinak by to ani nesedělo dimenzema. Divergence musí být z vektoru. Skalární součiny značím výhradně  , normální součiny neznačím, dost mi to pomáhá.
, normální součiny neznačím, dost mi to pomáhá.