Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Věta o izomorfismu? (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 07. 2014 21:48
Věta o izomorfismu?
Ahoj, mám takovýhle problém: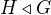 jsou grupy a je
jsou grupy a je  . Pro
. Pro  existuje
existuje ![kopírovat do textarea $K\in [H,G]$](/mathtex/60/6094d1d99b2d67d966bf962e80b9c198.gif) ,
,  taková, že
taková, že  . Je taky
. Je taky  ?
?
Prosím o radu.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 08. 07. 2014 22:52
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Věta o izomorfismu?
↑ Andrejka3:
Ahoj, co je to prosím [H,G]? (Podle kontextu to bude nějaká množina grup, ale jaká?) Děkuji za informaci.
PS: Jde o konečné, nekonečné grupy a nebo to nechceš rozlišovat?
"Máte úhel beta." "No to nemám."
Offline
#3 09. 07. 2014 00:03 — Editoval Andrejka3 (09. 07. 2014 02:13)
Re: Věta o izomorfismu?
↑ check_drummer:
Ahoj, [H,G] je myšlen interval ve svazu (normálních) podgrup grupy G. Takže jen tohle  .
.
Jinak stačí pro konečné grupy. Původně jsem měla dotaz specifický, ale raději jsem to napsala obecnější.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 09. 07. 2014 23:43
Re: Věta o izomorfismu?
Ahoj.
Nie som si celkom istý, ale mohlo by to byť nasledovne:
Môžme použiť tretiu vetu o izomorfizme, 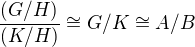 , a teda
, a teda  je normálna podgrupa. Dostaneme komutatívny diagram:
je normálna podgrupa. Dostaneme komutatívny diagram:
prvá časť:  ;
;
druhá časť:  .
.
Odtiaľ vidno, že obraz (K/H) v grupe A je podmnožinou množiny B a je aj normálnou podgrupou v A, vďaka izomorfizmu.
Pre ľubovolnú normálnu podgrupu B grupy A, vezmeme jej obraz v grupe (G/H) [izomorfizmus], ktorý je normálnou podgrupou, a označme ho K. Potom sa použije ten predošlý odstavec a malo by to sedieť.
Offline
#5 10. 07. 2014 00:23
Re: Věta o izomorfismu?
↑ :D:
Děkuji za odpověď. Byl bych ráda za trochu podrobnější rozpis. Takhle si myslím, že to neověřím, ale děkuji za nápad, budu o tom přemýšlet.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 10. 07. 2014 11:52 — Editoval OiBobik (10. 07. 2014 11:57)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Věta o izomorfismu?
↑ Andrejka3:
Ahoj,
určitě ne nutně, ale vždycky takovou  lze najít.
lze najít.
1) Proč ji lze najít: to je v podstatě jen věta o korespondenci spolu s třetí (druhou?) větou o isomorfismu (myslím, že to je to, o čem píše ↑ :D:).
2) Ale stále může existovat pro  normální podgrupa
normální podgrupa ![kopírovat do textarea $K\in [H,G]$](/mathtex/60/6094d1d99b2d67d966bf962e80b9c198.gif) tak, že vše, co píšeš, platí, až na závěr
tak, že vše, co píšeš, platí, až na závěr  : stačí vzít
: stačí vzít 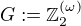 (tj spočetná dir. suma kopií
(tj spočetná dir. suma kopií 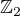 )
)  , tedy
, tedy  . Pak zvolíme-li
. Pak zvolíme-li  (tj podgrupa
(tj podgrupa  taková, že všechny její prvky mají nenulovou nejvýše první souřadnici; tj "první kopie"
taková, že všechny její prvky mají nenulovou nejvýše první souřadnici; tj "první kopie" 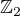 v té dir. sumě), dostaneme, že
v té dir. sumě), dostaneme, že 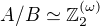 , tedy lze volit
, tedy lze volit  . Pak
. Pak  , ale
, ale  .
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#7 10. 07. 2014 13:07 — Editoval Andrejka3 (10. 07. 2014 13:08)
Re: Věta o izomorfismu?
↑ OiBobik:
Díky za odpověď, ten můj dotaz souvisí s nějakou oblastí teorie grup, kterou asi neznám? Ten protipříklad Tě napadnul nějakým elementárním přemýšlením, nebo je za tím hlubší teorie?
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 11. 07. 2014 09:24 — Editoval OiBobik (11. 07. 2014 10:38)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Věta o izomorfismu?
↑ Andrejka3:
Nějaká extra teorie k tomu mě asi moc nenapadá... Ten příklad člověk vymyslí tak nějak elementárně (moje intuice za tím je "dostatečně vysoká grupa, tak, že faktorizace někde dole se ztratí"; možná esteticky lepší příklad téhož typu je vzít si Prüferovu grupu, tj, pro  prvočíslo, něco jako
prvočíslo, něco jako ![kopírovat do textarea $\mathbb{Z}[\frac{1}{p}]/\mathbb{Z}$](/mathtex/30/30f467d6f2e434e822c9eb54e07f722e.gif) se sčítáním, resp
se sčítáním, resp 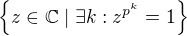 s násobením, což je totéž - pak dokonce faktor podle libovolné vlastní podgrupy je isomorfní původní grupě).
s násobením, což je totéž - pak dokonce faktor podle libovolné vlastní podgrupy je isomorfní původní grupě).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#9 11. 07. 2014 11:01
Re: Věta o izomorfismu?
↑ OiBobik:
Jasně, pamatuju si, že jsi mě na to už jednou upozorňoval :)
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Věta o izomorfismu? (TOTO TÉMA JE VYŘEŠENÉ)
 konečná. Nechť
konečná. Nechť  je komutativní (konečná). Pak
je komutativní (konečná). Pak  . Je
. Je  a jeho faktor je izomorfní
a jeho faktor je izomorfní  . Podle věty o izomorfismu této normální podgrupě odpovídá normální podgrupa
. Podle věty o izomorfismu této normální podgrupě odpovídá normální podgrupa ![kopírovat do textarea $K\in [H,G]_{\mathbf{Sub}_{\mathrm{N}}G}$](/mathtex/67/67c709618fc8aa4df99524cb5660d4a2.gif) , přičemž je
, přičemž je 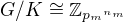 . Je
. Je 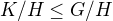 , tedy podgrupou komutativní grupy
, tedy podgrupou komutativní grupy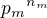 , tedy řádu
, tedy řádu  . Nyní pokračujeme zjemňováním řady
. Nyní pokračujeme zjemňováním řady  , až všechny faktory mezi
, až všechny faktory mezi  a
a  . Dokázat to třeba není, ale taky se mi to nepovedlo.
. Dokázat to třeba není, ale taky se mi to nepovedlo. je normální řada
je normální řada  je normální řada derivací
je normální řada derivací  . Ale zjemnění
. Ale zjemnění  má pouze cyklické faktory. Kdyby řada derivací končila netriviální dokonalou grupou (druhý nejmenší prvek
má pouze cyklické faktory. Kdyby řada derivací končila netriviální dokonalou grupou (druhý nejmenší prvek  existovala její normální podgrupa, jejíž faktor by byl netriviální cyklickou grupou. Jediný její komutativní faktor je však triviální. To je spor. Řada derivací končí triviální grupou a je tedy řešitelná.
existovala její normální podgrupa, jejíž faktor by byl netriviální cyklickou grupou. Jediný její komutativní faktor je však triviální. To je spor. Řada derivací končí triviální grupou a je tedy řešitelná.