Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 07. 2015 23:28
- Contemplator

- Příspěvky: 362
- Reputace: 0
Kvadratická rovnica
Mám rovnicu: 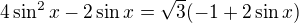 teda po úprave a subst.
teda po úprave a subst. 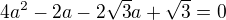 To čo chcem vedieť je, či sa ako člen -b- v kvadratickej rovnici bere
To čo chcem vedieť je, či sa ako člen -b- v kvadratickej rovnici bere 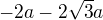 ?:)
?:)
Offline
- (téma jako vyřešené označil(a) jelena)
#3 11. 07. 2015 09:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kvadratická rovnica
Zdravím,
pohodlnější pro řešení je hned od zadání 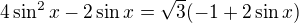 vytknout
vytknout 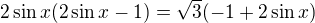 a následně upravit na součinový tvar s anulovanou pravou stranou (nebo obdobně lze provést i v substituovaném návrhu, ale je zde zavedení substituce zbytečné). Je tak? Děkuji.
a následně upravit na součinový tvar s anulovanou pravou stranou (nebo obdobně lze provést i v substituovaném návrhu, ale je zde zavedení substituce zbytečné). Je tak? Děkuji.
Offline
#4 11. 07. 2015 12:00
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Kvadratická rovnica
No, vyzerá že je:) Ďakujem, to som nevidel, a gadgetka tam vlastne ani nie je treba vynímať  nie? stačí to len s číslami spraviť, tak ako netreba substitúciu:)?
nie? stačí to len s číslami spraviť, tak ako netreba substitúciu:)?
Offline
#5 11. 07. 2015 12:02 — Editoval krauva (11. 07. 2015 12:05)
Re: Kvadratická rovnica
Ahoj, je mi jasné, že řešení vytýkáním je snažší, ale pokud bychom to řešili přes diskriminant, tak pak pro x platí: 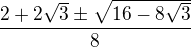 . Jak tento výraz upravím, abych dostal hezké kořeny jako
. Jak tento výraz upravím, abych dostal hezké kořeny jako  ? Dík
? Dík
PS: jde mi jen hlavně o tu odmocninu rozdílu v čitateli...
Offline
#7 11. 07. 2015 12:11 — Editoval Al1 (11. 07. 2015 12:15)
Re: Kvadratická rovnica
↑ Contemplator:
Zdravím,
vytknutí proměnné a v tvém postupu je nutné pro správné určení koeficientů kvadratické rovnice. Substutice není nutná, pokud dobře chápeš princip řešení kvadratické rovnice, prostě napíšeš, že 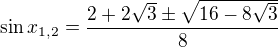
Poznámka: je nešikovné volit v substituci za proměnnou sinx proměnnou a (nebo b či c), pak se mohou plést tyto s koeficienty kvadratické rovnice dosazované do vzorce pro diskriminant. Zkušeným počtářům to ovšem samozřejmě nevadí.
Offline
#9 11. 07. 2015 13:59
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Kvadratická rovnica
Jasné, rozumiem, ale ešte jedna vec k podobnému príkladu: 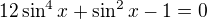
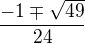
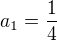
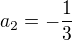
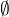
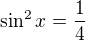
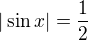
Výsledok je pre: 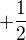 pre - nie Nemalo by byť správne aj:
pre - nie Nemalo by byť správne aj: 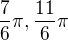 ?
?
Offline
#10 11. 07. 2015 14:07
Re: Kvadratická rovnica
↑ Contemplator:
řešením je 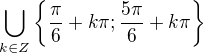 , které obsahuje i hodnoty pro řešení rovnice
, které obsahuje i hodnoty pro řešení rovnice 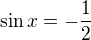
Offline
#11 11. 07. 2015 14:33
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Kvadratická rovnica
Ďakujem, už som sa uvedomil, to zase preto, že som si to nanačrtol...
Offline

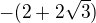 , což je koeficient
, což je koeficient  kvadratické rovnice.
kvadratické rovnice.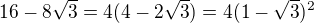 a nyní již diskriminant odmocníš hravě.
a nyní již diskriminant odmocníš hravě.