Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz o "právě jednom řešení" (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 09. 2015 02:05
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Důkaz o "právě jednom řešení"
Ahoj všichni!
Snažím se dostat do "důkazových" úloh, kterým jsem se doteď prakticky nevěnoval - na VŠ jsem se učil spíše algoritmy výpočtů pro konkrétní příklady, popř. se na hodině vysvětlila indukce a pár úloh na nepřímý důkaz a spor. Nejsem si tedy jistý u řešení následujícího příkladu:
Zadání:
V - vektorový prostor (pro zjednodušení značím jen takhle a ne korektně  )
)
Dokažte, že pro KAŽDÉ 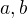 má rovnice PRÁVĚ JEDNO řešení, a to
má rovnice PRÁVĚ JEDNO řešení, a to  .
.
Můj postup:
1) Chci dokazovat něco o "právě jednom", tedy zkusím nejdřív důkaz sporem.
2) Předpokládám tedy 2 různá řešení místo jednoho: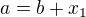
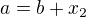

3) Upravím si  na
na  .
.
4) 
Dosadím za "a" dle druhého řádku předpokladu (bod 2 řešení).
Upravím výraz.
5) Získal jsem tedy spor: (bod 4 řešení)
(bod 4 řešení) (3 řádek předpokladu - bod 2 řešení)
(3 řádek předpokladu - bod 2 řešení)
Dá se to řešit nějak takhle nebo na to jdu úplně blbě?
Moc díky za všechny rady,
Katsu.
Offline
- (téma jako vyřešené označil(a) Katsushiro)
#2 14. 09. 2015 14:34
Re: Důkaz o "právě jednom řešení"
↑ Katsushiro:
Ahoj.
Důkaz jednoznačnosti řešení rovnice  by tímto způsobem, myslím, šel,
by tímto způsobem, myslím, šel,
ale není tím vyřešena otázka existence řešení.
Podívej se na axiomy vektorového prostoru, například zde, odstavec Definice vektorového prostoru.
Offline
#3 14. 09. 2015 15:15
Re: Důkaz o "právě jednom řešení"
Ahoj ↑ Katsushiro:, ↑ Rumburak:
Ak ide o riesenie rovnice x+b=a
tak staci si uvedomit, ze ide o rovnicu v komutativnej grupe (V,+).
Akoze, v structure grupy, operacia + je dobre (jednoznacne ) defininovana. Naviac jej axiomy zarucuju existenciu opacneho prvku.
Preto vdaka standardnej (=beznej) axiomatike odpoved na dane otazky je automaticka.
Poznamejme, ze niekedy sa mozeme stretnut z inymi axiomatikamy structury grupy, no v tom (exotickom pripade) to treba upresnit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 15. 09. 2015 20:45 — Editoval kaja.marik (15. 09. 2015 20:46)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Důkaz o "právě jednom řešení"
Taky bych se jenom odvolal na to, ze (V,+) je komutativni grupa.
Pokud bych to rozepisoval, asi bych to lehce zkratili tim, ze bych nezduraznoval ze na to jdu sporem, nezduraznoval, ze  , ale predpokladal, ze
, ale predpokladal, ze  je reseni tvaru
je reseni tvaru  (dosazenim predtim overim, ze to reseni skutecne je) a potom predpokladal, ze
(dosazenim predtim overim, ze to reseni skutecne je) a potom predpokladal, ze  je jakelikov jine reseni a ukazal ze
je jakelikov jine reseni a ukazal ze  , presne jak to je v uvodnim prispevku. Tim je existence i jednoznacnost dokazana.
, presne jak to je v uvodnim prispevku. Tim je existence i jednoznacnost dokazana.
Offline
#5 18. 09. 2015 23:34
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Důkaz o "právě jednom řešení"
Moc všem díky ;-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz o "právě jednom řešení" (TOTO TÉMA JE VYŘEŠENÉ)