Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Dôkaz matematickou indukciou (2^n > n^2) (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 10. 2016 16:38 — Editoval Marek Mattos (19. 10. 2016 16:40)
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Dôkaz matematickou indukciou (2^n > n^2)
Dobrý deň. Chcel by som vás poprosiť či by sme mi nepomohli s dôkazom.
Zadanie: 
Zatiaľ som postupoval takto: T(5)

Pravda
Nech platí T(k)
T(k+1)

A tu som skončil. Viem že sa mám dostať z T(k) ku T(k+1) ale neviem aký ďalší krok mám spraviť.
Vopred ďakujem za rady.
Offline
- (téma jako vyřešené označil(a) Marek Mattos)
#2 19. 10. 2016 16:44
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Marek Mattos:
Za 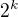 dosadíš z indukčního předpokladu T(k)
dosadíš z indukčního předpokladu T(k) 
Offline
#3 19. 10. 2016 16:49
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Elisa:
Ale vzťah medzi 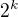 a
a  nieje rovnosť. Môžem to spraviť?
nieje rovnosť. Môžem to spraviť?
Offline
#4 19. 10. 2016 17:01 — Editoval vanok (19. 10. 2016 17:01)
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Marek Mattos:,
Indukcny krok.
Mas dokazat  T(k+1) za predpokladu
T(k+1) za predpokladu  T(k).
T(k).
T(k) po nasobenie 2mi ti da (1)
(1)
No vsak vsak  ti da co? Plati pre
ti da co? Plati pre  ?
?
Pouzi to v (1).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 19. 10. 2016 17:26
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
T(5)

Pravda
Nech platí T(k) pričom 

T(k+1)



To je ako celý dôkaz?
Offline
#6 19. 10. 2016 17:33
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Marek Mattos:,
To co pises nie je dokaz.
Tvoj ciel:
Vdaka relacii (1) musis dokazat T(k+1).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 19. 10. 2016 18:06
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
Ďakujem za pomoc.
Môžete zamknúť túto tému.
:)
Offline
#8 19. 10. 2016 18:27 — Editoval vanok (20. 10. 2016 03:01)
Re: Dôkaz matematickou indukciou (2^n > n^2)
To ty zamkni ak myslis ze mas riesenie.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 19. 10. 2016 21:20
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Elisa:
To zavisi od postupu a metody pouzitej v cviceni.
Tu potrebne konecne upravy nie su napisane. ... tu pouzita metoda je pouzitie vhodnej nerovnosti, no chyba este jej dokaz a jej aplikacia v cviceni.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 19. 10. 2016 22:12
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Elisa:
Podle indukčního předpokladu platí  a teď by se nám náramně hodilo, kdyby platilo
a teď by se nám náramně hodilo, kdyby platilo  . Platí to (za daných předpokladů)? Jak z toho plyne výsledek?
. Platí to (za daných předpokladů)? Jak z toho plyne výsledek?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#13 20. 10. 2016 09:51
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ byk7:
Za daných prepokladov myslíš že k+1=n?
Offline
#14 20. 10. 2016 09:59
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Marek Mattos:,
Nie. Precitaj si cele vlakno.
Len ako som ti uz pisal vyssie, ↑ vanok: je treba doplnit tvoj dokaz.
No vsak si napisal ↑ Marek Mattos: tak to znamena, ze mas tvoje riesenie... A teraz sa pytas o co ide.
Na realizovanie indukcbeho kroku potrebujes dokazat, ze pre 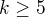 mas
mas  .
.
Tak napis ako si to urobil?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 20. 10. 2016 17:13
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ vanok:
ja som do tej svojej poslednej nerovnice dosadil iba číslo 5 a myslel som si že to stačí. 
25 > 11 platí tak som potom skončil
takže musím teraz ešte dokázať že 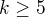 aj keď som na začiatku definoval že n = k a viem že n bude mať hodnoty iba nad 5?
aj keď som na začiatku definoval že n = k a viem že n bude mať hodnoty iba nad 5?
Offline
#16 20. 10. 2016 17:17 — Editoval vanok (20. 10. 2016 17:18)
Re: Dôkaz matematickou indukciou (2^n > n^2)
Nie treba to mat vseobecne.
Napr. Poslednu nerovnost napis este takto 
A potom ukazat ze to je plati ak 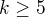 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 20. 10. 2016 17:28
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
takže si to upravím na 
a keďže 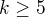 tak dosadím za k číslo 5
tak dosadím za k číslo 5

pravda
Spravil som to dobre? Treba ešte niečo?
Offline
#18 20. 10. 2016 17:57 — Editoval vanok (20. 10. 2016 17:59)
Re: Dôkaz matematickou indukciou (2^n > n^2)
Skor musis povedat, ze nerovnost plati lebo mas zaroven  a
a 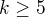 , A tak ju mozes pouzit v ton indukcnom kroku.
, A tak ju mozes pouzit v ton indukcnom kroku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 20. 10. 2016 18:13
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
A už nič viac nieje potreba?
Offline
#20 20. 10. 2016 18:24 — Editoval vanok (20. 10. 2016 18:43)
Re: Dôkaz matematickou indukciou (2^n > n^2)
↑ Marek Mattos:
Teraz mozes napisat ten dokaz.
Indukcny krok.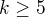
Mame dokazat  T(k+1) za predpokladu
T(k+1) za predpokladu  T(k).
T(k).
T(k) po nasobenie 2mi ti da (1)
(1)
No vsak vsak  ( to sme prave dokazali)
( to sme prave dokazali)
Tak (1) da Co je T(k+1)
Co je T(k+1)
Vidis co bolo treba
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 20. 10. 2016 18:44
Re: Dôkaz matematickou indukciou (2^n > n^2)
Ahoj ↑ byk7:,
Dakujem preklep opraveny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 22. 10. 2016 20:31
- Marek Mattos

- Příspěvky: 45
- Pozice: student
- Reputace: 1
Re: Dôkaz matematickou indukciou (2^n > n^2)
Ďakujem za pomoc. :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Dôkaz matematickou indukciou (2^n > n^2) (TOTO TÉMA JE VYŘEŠENÉ)
