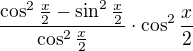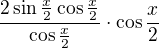Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#10 29. 12. 2016 18:58
Re: integrace
↑ Elisa:,
Poznamka. Tvoj vypocet mozes zacat aj z tym, ze vyuzijes ze  ... no celkovo sa zda, ze to nie je rychlejsie ako predosla navrthnuta, velmi klasicka metoda.
... no celkovo sa zda, ze to nie je rychlejsie ako predosla navrthnuta, velmi klasicka metoda.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 30. 12. 2016 09:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrace
Zdravím,
↑ vanok: asi překlep ve vzorci (kontrolovala jsem ve WA, z hlavy si to samozřejmě nepamatuji). JInak by šel použit pěkně na rozšíření a na další úpravy.
Goniometrické substituce (zejména  je univerzální) a obvykle pomohou (i strojově, tuším, jsou využívány primárně), ale takové ne dost kreativní :-), viz výš v tématu navržené úpravy. Zde se mi zda také možné provést rozšíření:
je univerzální) a obvykle pomohou (i strojově, tuším, jsou využívány primárně), ale takové ne dost kreativní :-), viz výš v tématu navržené úpravy. Zde se mi zda také možné provést rozšíření:
Pro první 2 zlomky platí úprava v odkazu - příklad C, pro poslední dva zlomky lze použit substituci. Spíš na doplnění, když po ruce nebude odvození goniometrických substituci.
Offline