Matematické Fórum

↑↑ Eratosthenes:
Přesně tak, takže to, že "a=a" má smysl není kvůli tomu, že je součástí gramaticky správné formule "a=a+1 => a=a", jak jsi uváděl, ale díky tomu, že je to gramaticky správná formule. Abys totiž mohl říci, že je implikace gramaticky správná formule, tak musí být její předpoklady a závěry gramaticky správné formule.

Ahoj, výraz chápu jako negaci .

Dále si myslím, že pokud nějaký výraz neexistuje, tak by jej v prvé řadě člověk neměl vůbec psát. Tj. např. než napíšu , tak bych měl nejprve vyšetřit chování funkce a dokázat, že uvedená limita existuje.

Z mého pohledu je tedy zápis typu nesprávný ne proto, že by nebyla negace , ale proto, že již podvýraz je nesprávný a IMHO nemá v pečlivě napsaném textu co dělat.

↑ Eratosthenes:

Pokud správně počítám (pomocí Taylorova rozvoje), platí , takže proti uvedenému výrazu nic nemám :-)

Nicméně bych rád korigoval svůj předchozí příspěvek ↑ bedrnik:, kde jsem psal, že výraz typu je nesprávný a v žádném případě nemá v matematickém textu co dělat. To je příliš silné tvrzení, např. nevidím nic špatného na větě: " neexistuje."

Přesto však trvám na tom, že výrazy typu nebo 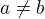jsou matoucí, pokud nebo není dobře definovaný matematický objekt.

Takže je podle mě správně napsat např.: "Pokud existuje, pak ." Na druhou stranu bych nepsal rovnou bez dalšího vysvětlení, protože hrozí, že si to čtenář vyloží tak, že uvedená limita existuje (a nerovná se 1).

↑ Rumburak:
Ahoj. Děkuji za upozornění, měl jsem na mysli ZF. Ale jak píšeš, lze obě teorie na sebe "převést". Jestli to tedy chápu správně, tak i na třídu jsou kladena jistá omezení - např. si myslím, že neexistuje třída, která je prvkem sama sebe, že?
A z té definice se mi zdá, že vlastní třídy (na rozdíl od množin) netvoří hierarchickou strukturu, tj. že vlstní třída nemůže být prvkem jiné třídy (ať už vlastní nebo nevlastní).

↑ check_drummer:

ad 1) Výraz existuje vždy. Existovat začne v okamžiku, kdy se napíše :-) Takže jednoznačně tvoje dvojka. Je totiž třeba rozlišovat to, co stále nerozlišuje ↑ bedrnik: : totiž výraz správný syntakticky a výraz správný sémanticky.  Syntakticky správný výraz je výraz napsaný podle pravidel ("gramaticky správný") a výraz správný sémanticky je to, co existuje, resp. pravdivá informace o existujícím objektu ("pravdivý výrok").

Výraz a+a = 2a je správný syntakticky i sémanticky.

Výraz a+1 = a je správný syntakticky. Má smysl, je rozumět, co tím chtěl autor říci. Není správně sémanticky (takové číslo neexistuje). Ale má smysl to napsat a má smysl se o tom bavit - viz složitější případy limit, nebo ↑ Eratosthenes:.

Výraz a== není správně ani sémanticky ani syntakticky. Je nepochopitelný, není jasné, co tím chtěl autor říci. Nemá smysl takové sekvence psát a o takových zápisech se bavit, až snad na výjimečné případy - např. metajazykové souvislosti - mohu ho uvést např. v učebnici logiky jako příklad syntakticky nesprávné formule.

↑ check_drummer:


Ahoj.

Podrobnou axiomatiku CB teorie tu jen tak z patra nepodám - snad bude k nalezení na webu.

Smozřejmě, ani vlastní třída nemůže být prvkem sama sebe. Kdyby tomu tak bylo, muselo by
nutně jít o množinu (třída, která je zároveň  prvkem v nějaké třídě,  je dle definice v CBTM množinou). 
Že množina nemůže být svým vlastním prvkem, je rovněž vyřešeno.