Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 12. 2017 12:04
Pravouhle trojuholniky
Pozdravujem.
Nech a,b,c su celociselne dlzky stran pravouhleho trojuholnika. Dokazte, ze aspon jedno z cisiel a, b, c je delitelne cislom 5.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 20. 12. 2017 20:08 — Editoval vanok (20. 12. 2017 20:19)
Re: Pravouhle trojuholniky
Ahoj ↑ kerajs:,
To je dobra kostra riesenia. Co by bolo uzitocne je slovny doprovod.
Ina moznost je dokaz sporom.(Mozme predpokladat, ze sucin 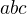 nie je delitelny cislom 5 a vysetrit co to da v pripade, ked
nie je delitelny cislom 5 a vysetrit co to da v pripade, ked  .)
.)
Kto ma chut moze to skusit.
Poznamka. Je velmi uzitocne pisat matematicke dokazy tak aby vasi citatelia mohli pochopit vasu pracu. Tu sa mozte trochu poucit o tom http://cheng.staff.shef.ac.uk/proofguide/proofguide.pdf
Na webe najdete viacero dobrych rad na tu temu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 22. 12. 2017 07:17 — Editoval Honzc (22. 12. 2017 07:20)
#5 22. 12. 2017 12:26 — Editoval vanok (22. 12. 2017 14:12)
Re: Pravouhle trojuholniky
Ahoj ↑ Honzc:,
Krasne Vianoce,
Pochopitelne to je tiez zaujimavy dokaz. ( za podmienky, ze su zname rovnosti tykajuce sa p.t.). Vyhoda je v tom, ze ide o priamy dokaz a stredoskolaci niekedy nemaju radi dokazy sporom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 23. 12. 2017 21:38
- check_drummer

- Příspěvky: 4972
- Reputace: 106
Re: Pravouhle trojuholniky
↑ Honzc:
Ahoj. Pokud předpokládáme, že středoškoláci znají modulární aritmetiku, jde to snadněji:
"Máte úhel beta." "No to nemám."
Offline
#7 03. 01. 2018 04:30
Re: Pravouhle trojuholniky
Pozdravujem ↑ check_drummer:,
Najkrajsie zelania no Noveho Roku 2018.
Tvoja odpoved je citatelna mnohymi stredoskolakmi.
A tiez mi dala myslienku k
Dokazte, ze sucin abc je vzdy delitelny cislom 60, ( a, b, c su ako v cviceni v ↑ vanok:)
Co sa tyka poslenych dvoch riadkov ↑ check_drummer:, o generovani takych trojuholnikov dal v 1934 odpoved Berggren (cf. Génération algébrique et géométrique)
ako sa to mozeme dozvediet z https://fr.m.wikipedia.org/wiki/Triplet_pythagoricien
kde sa najde vela zaujimavych veci na tuto temu, ako aj v anlickej verzii.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 13. 01. 2018 14:43
- check_drummer

- Příspěvky: 4972
- Reputace: 106
Re: Pravouhle trojuholniky
↑ vanok:
Se zpožděním přeji rovněž vše nejlepší do nového roku 2018.
Já jsem někdy něco podobného četl, ale nemohl jsem si vzpomenout, jk to generování probíhalo.
"Máte úhel beta." "No to nemám."
Offline


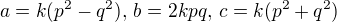

 nebo
nebo 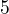 , pak výraz
, pak výraz 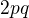 končí číslicí
končí číslicí 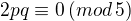 -a tedy alespoň jedna ze stran p.t. je dělitelná pěti.
-a tedy alespoň jedna ze stran p.t. je dělitelná pěti.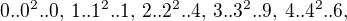
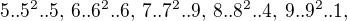
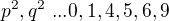

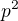 a
a 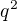 stejné, pak
stejné, pak 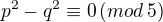 -a tedy alespoň jedna ze stran p.t. je dělitelná pěti.
-a tedy alespoň jedna ze stran p.t. je dělitelná pěti.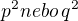 končí číslicemi
končí číslicemi 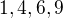
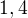 Pak
Pak 
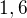 Pak
Pak 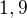 Pak
Pak 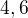 Pak
Pak 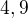 Pak
Pak 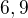 Pak
Pak 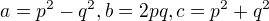 .
.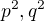 stejnou paritu, pak 5 dělí a, a pokud mají různou paritu, tak 5 dělí c.
stejnou paritu, pak 5 dělí a, a pokud mají různou paritu, tak 5 dělí c.