Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 04. 2018 18:24
inverzná funkcia k logaritmu
Ahoj,
mám tu nasledujúce tvrdenie:
mám pocit, že tvrdenie v podčiarknutej časti nie je správne, pretože 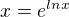
Viem že ma to takto učili, ale neviem presne prečo...dalo by sa to rozpísať krok po kroku ako to funguje, pretože do toho nejak nevidím....
ďakujem.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
- (téma jako vyřešené označil(a) Peter_CSR)
#2 06. 04. 2018 18:27 — Editoval vlado_bb (06. 04. 2018 18:27)
#4 06. 04. 2018 18:47
Re: inverzná funkcia k logaritmu
Aha, ja som si myslel že log značí dekadický logaritmus.
ok.
čo som svojou otázkou skôr myslel je prečo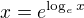
platí ale už 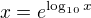
neplatí...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#5 06. 04. 2018 18:53
Re: inverzná funkcia k logaritmu
↑ Peter_CSR: Pretoze dekadicky logaritmus nie je inverzna funkcia k 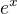 .
.
Offline
#6 06. 04. 2018 18:56
Re: inverzná funkcia k logaritmu
Zdravím, toto je zřejmě to, co tě učili a cos už zapomněl:
mějme  , pak platí, že
, pak platí, že 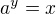 . Když dosadíme za
. Když dosadíme za  , dostaneme:
, dostaneme: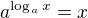
:)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 06. 04. 2018 18:59
Re: inverzná funkcia k logaritmu
gadgetka napsal(a):
Zdravím, toto je zřejmě to, co tě učili a cos už zapomněl:
mějme, pak platí, že
. Když dosadíme za
, dostaneme:
:)
ah, toto som hľadal. ďakujem ! :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#8 06. 04. 2018 19:00
Offline
#9 06. 04. 2018 19:01
Re: inverzná funkcia k logaritmu
↑ gadgetka:
chápem správne, že toto je zároveň aj dôkazom inverznej funkcie k logaritmu.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#10 06. 04. 2018 19:06
Re: inverzná funkcia k logaritmu
Ano, protože logaritmus je exponent, na který musíme umocnit základ, abychom dostali argument x. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#11 06. 04. 2018 19:06
Re: inverzná funkcia k logaritmu
↑ gadgetka:
presne tak, vdaka :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline

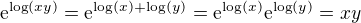
 se ve velke casti sveta znaci prirozeny logaritmus
se ve velke casti sveta znaci prirozeny logaritmus 
