Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Barycentricke suradnice
#1 20. 03. 2018 17:48
Barycentricke suradnice
Pozdravujem,
Mala otazka.
Co viete o barycentrickych suradniciach?
Kedy a na akej urovni ste sa o tomto pojme dozvedeli?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#3 20. 03. 2018 19:09 — Editoval vanok (21. 03. 2018 09:12)
Re: Barycentricke suradnice
Ahoj ↑ laszky:,
Ano, ale v akom ramci?
A co vies o barycentrickyrh rovnicach?
Ake problemy vies riesit?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#4 21. 03. 2018 09:10 — Editoval vanok (27. 02. 2021 11:15)
Re: Barycentricke suradnice
Pridam tu, co iste kazdy vie.
V minulom storoci sa tento pojem vyucoval uz aj na SS. Niekto ma na to spomienky?
Pripomenme definiciu v pripade afinnej roviny. ( Def. je tak platna aj v euklidovskej rovine).
Nech
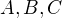 su tri body roviny ktore nie su na jednej priamke. Potom trojica
su tri body roviny ktore nie su na jednej priamke. Potom trojica  sa vola referencny trojuholnik.
sa vola referencny trojuholnik. Potom bod
 tejto roviny, trojica
tejto roviny, trojica  taku, ze
taku, ze  a
a  sa vola
sa vola barycentrum vazenych bodov
 .
.Je jasne, ze trojica
 ako aj trojica
ako aj trojica  definovana ako nenulovy nasobok predoslej vyhovuje danej definicii. ( cize barycentrum nie je jednoznacne urcene, a ho budeme volat barycentricke suradnice bodu
definovana ako nenulovy nasobok predoslej vyhovuje danej definicii. ( cize barycentrum nie je jednoznacne urcene, a ho budeme volat barycentricke suradnice bodu  ).
).Niekedy moze byt prakticke vybrat take barycentricke suradnice, ze
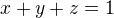 , vtedy hovorime o normalizovanych barycentrickych suradniciach bodu
, vtedy hovorime o normalizovanych barycentrickych suradniciach bodu  .
.Na pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#5 22. 03. 2018 07:25 — Editoval vanok (27. 02. 2021 11:18)
Re: Barycentricke suradnice
Pokracovanie.
Lahko odvodime,ze pre lubovolny bod roviny 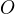 plati ekvivalentne
plati ekvivalentne
 .
.
Pochopitelne, lahko sa sa daju vyjadrit vzorce ako prejt z afinnych suradnic do barycenttickych a opacne.
Urcite to viete urobit
Kontrola
Na pokracovanie...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#6 23. 03. 2018 10:28 — Editoval vanok (25. 03. 2018 07:08)
Re: Barycentricke suradnice
Pokracovanie 2.
Tak teraz je jasne pre kazdeho, ze body roviny vzladom k referecnemu trojuholniku  z barycentrickymi suradnicami
z barycentrickymi suradnicami  su take, ze
su take, ze  .
.
Tiez je bezne oznacit normalizovane barycentricke suradnice taketo bodu 
Teraz si polozme otazku: na co moze sluzit rovnost 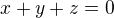 ?
?
Je zaujimave konstatovat, ze pre trojicu  realnych cisiel taku, ze
realnych cisiel taku, ze 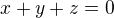 vektor
vektor  je nezavisly od bodu M.
je nezavisly od bodu M.
Kontrola
A reciprocne pre kazdy vektor
 ho vieme napisat vo forme
ho vieme napisat vo forme  kde
kde 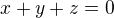
Co tiez znamena ze
 je bijektivna aplikacia. Tiez tato trojica sa vola barycentrike suradnice vektoru
je bijektivna aplikacia. Tiez tato trojica sa vola barycentrike suradnice vektoru  ....
....Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#7 25. 03. 2018 07:05 — Editoval vanok (25. 03. 2018 07:07)
Re: Barycentricke suradnice
Pokracovanie 3.
Pripomeniem este ze v euklidovskej orientovanej rovine mozme vyjadrit orientovanu plochu trojuholnika MNP vyrazom ![kopírovat do textarea $\frac 12 [\overrightarrow{MN},\overrightarrow{MP}]$](/mathtex/ea/ea4883a51bd8dac93c4ea7d6e6d5ca51.gif) kde
kde ![kopírovat do textarea $[.,.]$](/mathtex/5b/5b0b66c87da224aab4a31e326caf1da3.gif) je determinant vektorov v ortonormalnej priamo orientovanej baze.
je determinant vektorov v ortonormalnej priamo orientovanej baze.
Da sa dokazat, ze: Nech  je referencny trojuholnik v afinnej euklidovskej orientovanej rovine. Trojica
je referencny trojuholnik v afinnej euklidovskej orientovanej rovine. Trojica  baryceentrickych suradnic bodu
baryceentrickych suradnic bodu  je umerna trojici orientovanych ploch
je umerna trojici orientovanych ploch 
Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#8 26. 03. 2018 21:38
Re: Barycentricke suradnice
Pokracovanie 4
Tu najdete ten slubeny dokaz
Teraz mate vsetko aby ste vedeli nast, vdaka pojmom co som vam pripomenul, ze v trojuholniku ABC ( v euklidovskej rovine) nast jeden vnutorny bod taky, aby sucet ich vzdialenosti na druhu od stran trojuholnika
 bol minimalny.
bol minimalny. Tento sa vola Lemoine-ov bod. To vam necham radost urobit.
V buducom pokracovani osviezim vase spomienky o barycentrickych priamkach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#9 27. 03. 2018 22:26
Re: Barycentricke suradnice
Pokracovanie 5.
Pre kontrolu tu najdete odpoved na Lemoine-on bod.
Na pokracovanie si pripomenme, polynome
![kopírovat do textarea $ P \in \Bbb R [X,Y,Z]$](/mathtex/8d/8dd8f3224367f15aabb988b796ae514f.gif) je homogenny stupna
je homogenny stupna  ak mame
ak mame  , kde
, kde  est realne nenulove cislo.
est realne nenulove cislo. Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#10 13. 04. 2018 23:08
Re: Barycentricke suradnice
Pokracovanie 6.
Konstatujeme, ze  ....
....
A tak mnozina bodov M, barycentrickych suradnic (x,y,z) pre ktore plati P(x,y,z)=0 je dobre definovana (vsak su nezavysle od roznych barycentrickych suradnic toho isteho bodu). Mnozine takych bodov hovorime, ze  je jej barycentricka rovnica.
je jej barycentricka rovnica.
Je dolezite vediet prest z kartezianskych rovnic k barycentrickym a na opak.
Iste viete ako na to.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#11 14. 04. 2018 21:51 — Editoval vanok (27. 02. 2021 11:20)
Re: Barycentricke suradnice
Pokracovanie 7
Odpoved na posleddny riadok ↑ vanok:.
Ak GMB popisane v pokracovani 6 ma kartesiansku rovnicu  tak jeho barycentricka rovnica je
tak jeho barycentricka rovnica je  ( co sa da upravit).
( co sa da upravit).
Opacne, ak  je barycentricka rovnice toho GMB, tak jedne jeho kartesianska rovnica je
je barycentricka rovnice toho GMB, tak jedne jeho kartesianska rovnica je  .
.
Priklad pouzitia poslednych riadkov.
a)Priamka kartesianskej rovnice  ma barycentricku rovnicu
ma barycentricku rovnicu  co sa po zjednoduseni
co sa po zjednoduseni  .
.
b) Priamka kartesianskej rovnice  ma barycentricku rovnicu ( po zjednoduseni)
ma barycentricku rovnicu ( po zjednoduseni)  .
.
Ako sa pise kartezianska rovnica GMB ktore ma barycentricku rocnicu  ?
?
( neskor ukazem ze ide o kuzelosecku)
Ze je to jednoduche!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#12 23. 04. 2018 14:50 — Editoval vanok (29. 04. 2018 23:39)
Re: Barycentricke suradnice
Pokracovanie 8.
Ze ste nasli, po uprave,  .
.
Uvazujme teraz barycentricku rovnicu prveho stupna, ta je formy  , kde a,b,c nie su vsetki nulove.
, kde a,b,c nie su vsetki nulove.
Ake GMB representuje?
Ak mame 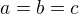 tak je ekvivalentna z
tak je ekvivalentna z  , co nijaky konecnyne vzdialeny bod nesplnuje. ( V toto pripade ide o barycentricku rovnicu priamky v nekonecne, projektivnej komplecie afinnej roviny).
, co nijaky konecnyne vzdialeny bod nesplnuje. ( V toto pripade ide o barycentricku rovnicu priamky v nekonecne, projektivnej komplecie afinnej roviny).
Tak predpokladajme ze nasa rovnica nie je takej formy.
Potom kartezianska rovnica GMB je formy  . ( co je skutocne kartezianska rovnica priamky lebo
. ( co je skutocne kartezianska rovnica priamky lebo  nie su obe nulove).
nie su obe nulove).
Podobne opacne mame [ doplnte si to]
Tak
Mnozina afinnych priamok roviny je dana barycentrickymi rovnicami formy  , kde
, kde  nie su sebe rovne.
nie su sebe rovne.
V buducych pokracovanachi pridam ( pre istotu ) zakladne vlasnosti a potom budete moct sami riesit vdaka tomu (zaujimave) cvicenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#13 29. 04. 2018 23:38
Re: Barycentricke suradnice
Pokracovanie 9.
Nech M , M’ su dva rozne body barycentrickych suradnic (x,y,z;); (x’,y’,z’), potom jedna barycentricka ronica priamky MM’ je napr.  , kde
, kde
p=yz’-y’z,
q=zx’—xz’,
r=xy’-x’y .
Pripomeniem tiez,ze
dve priamky  barymetrickych rovnic
barymetrickych rovnic
 su rovnobezne
su rovnobezne
ak 
Tymi istymi oznaceniami mame
Ak  nie su rovnobezne, potom ich spolocny bod ma barycentricke suradnice
nie su rovnobezne, potom ich spolocny bod ma barycentricke suradnice 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Barycentricke suradnice

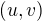 co znamena, ze
co znamena, ze  co nam okamzite da, ze
co nam okamzite da, ze 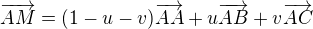 .
. su normalizovane barycentricke suradnice bodu
su normalizovane barycentricke suradnice bodu  , co nebudem stale opakovat ak je to jasne).
, co nebudem stale opakovat ak je to jasne). , co znamena...
, co znamena... Plati
Plati .
.![kopírovat do textarea $[ \overrightarrow{AM} ; x\overrightarrow{AM}+y\overrightarrow{BM}+z\overrightarrow{CM} ]=0$](/mathtex/a8/a851d1a23bd1b195a59d047b56392894.gif)
![kopírovat do textarea $y[\overrightarrow{AM};\overrightarrow{BM}]-z[\overrightarrow{CM};\overrightarrow{AM} ] =0$](/mathtex/43/43a974eb39a21df02ebbe9a4a41bb22f.gif)
 .
.