Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 27. 03. 2018 01:23
Re: Limitny maraton
↑↑ vanok:
Normalne ale existuji aj limity, ktore "neexistuji" :-) A kdyz pisete bez hacku a carek, tak slovo "rad" muze znamenat cesky nejenom "řada", ale take "řád". Potom by cele zadani nedavalo prilis smysl. Nehlede na to, ze se tu zrejme nejedna o lingvisticke forum, ale forum matematicke (to pokud byl zamer zmast resitele zadanim a zamernym neuvedenim symbolu sumace, ackoli je to bezne uzivany symbol).
Offline
#77 27. 03. 2018 06:02 — Editoval vanok (27. 03. 2018 08:30)
Re: Limitny maraton
Servus ↑ laszky:,
Nie, vsak takto sa bezne vsade pisu zadania cviceni. A diakriticke znzmienka nepisrm, lebo nemam sk mobil. Tak pisem ako mozem. Krasny den.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#78 27. 03. 2018 07:05
Re: Limitny maraton
Pozdravujem,
Dalsie cvicenie.
Cvicenie 19.
Dokazte, ze rad vseobecneho clenu 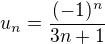 konverguje. Vypocitajte
konverguje. Vypocitajte 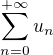
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#79 27. 03. 2018 08:29 — Editoval laszky (27. 03. 2018 17:26)
Re: Limitny maraton
Offline
#80 27. 03. 2018 08:34 — Editoval vanok (27. 03. 2018 08:37)
Re: Limitny maraton
Tschüs ↑ laszky:,
Si rychly ako blesk.
Z tebou sa foristi mozu dobre pripravit na skusky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#81 27. 03. 2018 08:51 — Editoval vanok (27. 03. 2018 10:02)
Re: Limitny maraton
Pozdravujem,
Cvicenie 20.
Vysetrite, ci limita 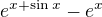 ked
ked  , existuje.
, existuje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#82 27. 03. 2018 16:33 — Editoval laszky (27. 03. 2018 16:38)
Re: Limitny maraton
Offline
#85 27. 03. 2018 22:00 — Editoval vanok (27. 03. 2018 22:01)
Re: Limitny maraton
Ahoj ↑ MichalAld:,
Aj rychlo riesitelne cvicenia sa davaju na skuskach. Tak podla tvojho zelania tu mas
Cvicenie 21.
Vysetrite, ci ma funkcia 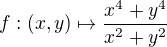 v bode
v bode  limitu. Ak ano najdite jej hodnotu. $
limitu. Ak ano najdite jej hodnotu. $
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#86 27. 03. 2018 23:36
Re: Limitny maraton
Offline
#88 28. 03. 2018 02:59 — Editoval vanok (28. 03. 2018 07:58)
Re: Limitny maraton
Bonsoir ↑ laszky:
Pridaj tam pred tvoj text : cvicenie 22.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#90 25. 04. 2018 05:10
Re: Limitny maraton
Offline
#91 25. 04. 2018 07:21 — Editoval vanok (25. 04. 2018 07:22)
Re: Limitny maraton
Pozdravujem.
Cvicenie 24.
Urcite  , kde
, kde  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#92 02. 05. 2018 22:01
Re: Limitny maraton
[re]p565431|vanok[/re
Pomoc pre cvicenie 24.
Mozte najprv ukazat, ze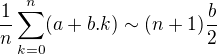 ak
ak 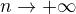 a tiez, ze
a tiez, ze pre
pre 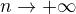 .
.
A tak vam potom ostane vysetrit 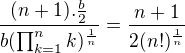
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#93 03. 05. 2018 07:16 — Editoval stuart clark (03. 05. 2018 07:40)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Nice ↑ vanok:.
Problem(25)
If ![kopírovat do textarea $l=\lim_{x\rightarrow 0}\frac{1}{x^m}\bigg[\left(\int^{x}_{0}(1-\cos t)dt\right)\left(\int^{x}_{0}(2-\cos 2t)dt\right)\left(\int^{x}_{0}(3-\cos 3t)dt\right)\cdots \left(\int^{x}_{0}(n-\cos nt)dt\right)\bigg]$](/mathtex/2c/2c5d1c47b1afbdcb080606f39f110e89.gif) exists finitely and
exists finitely and  . Then
. Then 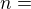 , where
, where 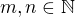 .
.
Offline
#94 03. 05. 2018 11:12
Re: Limitny maraton
Offline
#96 04. 05. 2018 09:25 — Editoval vanok (04. 05. 2018 09:30)
Re: Limitny maraton
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#98 05. 05. 2018 12:42 — Editoval vanok (05. 05. 2018 12:49)
Re: Limitny maraton
Hi ↑ stuart clark:,
Hint.
Let  .
.
Prove that 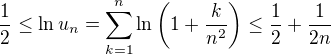
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#99 06. 05. 2018 15:12 — Editoval stuart clark (06. 05. 2018 15:12)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ vanok: I have also used that inequality  for all
for all  .
.
Then 
So Using Squeeze theorem
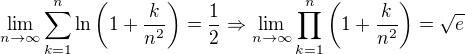
Offline
 ,
,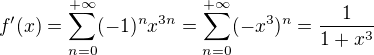 pro
pro  .
.
 .
.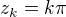 , pro
, pro 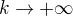 . Pak
. Pak 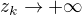 a
a 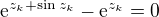 pro vsechna
pro vsechna  .
.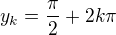 , potom opet
, potom opet 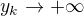 pro
pro  .
.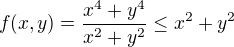 muzeme psat
muzeme psat![kopírovat do textarea $0\leq \lim_{(x,y)\to(0,0)} f(x,y) \leq \lim_{R\to 0} \left[ \max_{x^2+y^2\leq R^2} f(x,y)\right] \leq \lim_{R\to 0} R^2 = 0$](/mathtex/ee/eefd82b351b85474844f4205dab8a5e1.gif) ,
,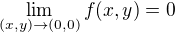 .
.
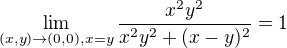

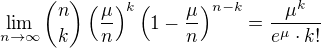
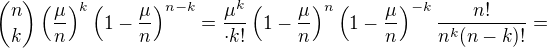

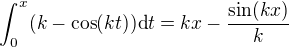 we have
we have 

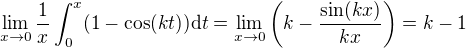 .
.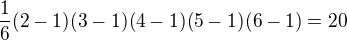 and that's why
and that's why 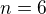 and
and 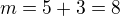 .
.

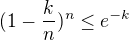 for
for  .
.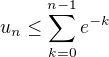
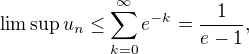
 in
in  .
.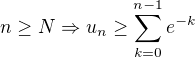 .
.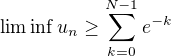
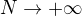 ,
,
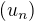 converges and
converges and 
 and ...😀
and ...😀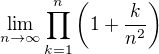
 .
.