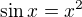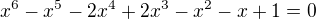Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Výhodné grafické řešení rovnic, nerovnic, soustav,...
#1 18. 11. 2018 11:31
Výhodné grafické řešení rovnic, nerovnic, soustav,...
Dobrý den,
mám za úkol vytvořit seminárku, ve které se zaměřím na výhodu grafického řešení u některých typů rovnic, nerovnic,soustavy rovnic a podobně. Nejlépe se mám zaměřit přímo na typy příkladů, které nejdou početně vyřešit, ale graficky ano. Případně ještě mohu doplnit příklady, které jdou sice početně vyřešit, ale grafické řešení je rychlejší a snazší. (k přesnému grafickému řešení můžu používat pc program, který už sem si vybral).
Zatím mě napadlo např.  a obdobné exponenciální rovnice - u těchto mi přijde, že početně je řešit nemůžeme (nebo alespoň s mou dosavadní gympláckou matematikou jsem na to nepřišel a zvládnu jen graficky).
a obdobné exponenciální rovnice - u těchto mi přijde, že početně je řešit nemůžeme (nebo alespoň s mou dosavadní gympláckou matematikou jsem na to nepřišel a zvládnu jen graficky).
Pak mě napadly některé rovnice s absolutní hodnotou např. 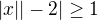 a podobné s absolutní hodnotou -tam některé sice vyřeším jak početně, tak graficky, ale grafické řešení mi přijde rychlejší.
a podobné s absolutní hodnotou -tam některé sice vyřeším jak početně, tak graficky, ale grafické řešení mi přijde rychlejší.
Bohužel mi nápady dochází a já bych měly vymyslet co nejvíce typů. Prosím, poradíte mi příklady, kde je grafické řešení ladnější nebo ještě lépe jediné možné? :)
Případně pokud na ně máte nějaký odkaz nebo něco podobného, tak bych byl moc vděčný.
Děkuji.
Offline
#3 18. 11. 2018 18:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výhodné grafické řešení rovnic, nerovnic, soustav,...
Zdravím,
přesunula jsem téma do Didaktiky, je to dobré podrobněji rozebrat.
že početně je řešit nemůžeme
neumíme zapsat řešení v "hezkém" tvaru, ze kterého jde zapsat řešení "pěkným" číslem, což však neznamená, že nejde řešit početně. V rovině gymplácké SŠ doporučuji se podívat na využití grafů funkcí pro numerická řešení nelineárních rovnic (to je příklad 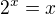 ), metody jako "půlení intervalu", "iterační metoda", "regula falsi", "metoda sečen" jdou zvládnou aparátem SŠ). A na tom si udělat jasno, proč grafické řešení zde není korektním řešením v plném smyslu tohoto slova. Materiály: Odkaz, Odkaz.
), metody jako "půlení intervalu", "iterační metoda", "regula falsi", "metoda sečen" jdou zvládnou aparátem SŠ). A na tom si udělat jasno, proč grafické řešení zde není korektním řešením v plném smyslu tohoto slova. Materiály: Odkaz, Odkaz.
Užití grafu pro řešení rovnic a nerovnic lze ukázat na (ne)rovnicích s absolutní hodnotou (jak jsi vybral(a)), také na goniometrických (ne)rovnicích a na dalších periodických, kde to hodně usnadní práci se zápisem řešení.
S první částí tématu bych byla ale opatrná :-) po zkušenosti, čímž zdravím i autora připomínky.
Offline
#4 18. 11. 2018 20:31
Re: Výhodné grafické řešení rovnic, nerovnic, soustav,...
Správný název je "které nelze řešit analyticky".
Obecně může jít o libovolnou funkci typu y = f(x) a z ní odvozenou rovnici f(x) = 0.
Jen ve velmi speciálních případech dokážeme najít x analytickým způsobem. Už jen u polynomů vyšších řádů (vyšších než 4) to analyticky nejde. A i pro řád 3 a 4 to jde těžko. Takže pro libovolný polynom se to může hodit.
A ke kdejaké trochu složitější kombinaci elementárních funkcí se nám inverzní funkci nepodaří nalézt taky.
Dále můžeš grafickou metodu používat na hledání řešení soustavy dvou rovnic, jako třeba:
y = f(x), y = g(x), čili f(x) = g(x). Je to sice to samé jako předchozí případ (protože můžeme napsat f(x) - g(x) = 0), ale pro grafické řešení to může být výhodnější tím druhým způsobem.
Grafické řešení má oproti numerickému velkou výhodu - víme, co vlastně děláme, a vidíme celý výsledek - takže třeba u polynomů z grafu hned vidíme, kolik má kořenů. Numericky se to zjišťuje těžko.
Jelena správně upozorňuje, že může dojít k problémům s přesností či zaokrouhlovacími chybami - ale to se může stát u numerického řešení celkem snadno taky.
Numerické metody jsou vhodné, když zhruba víme, kde máme řešní hledat, a chceme je najít s vysokou přesností. Grafické oproti tomu jsou dobré, když nevíme nic, a chceme se něco dozvědět. Ten graf nemusí nutně analyzovat člověk, mmch...může to dělat i AI (artificial intelligence).
Offline
#6 18. 11. 2018 20:56
Re: Výhodné grafické řešení rovnic, nerovnic, soustav,...
I při použití numerických metod můžeme dostat některé dost zajímavé výsledky, které stojí za to, aby byly zakresleny do grafu (Newtonův fraktál)
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Výhodné grafické řešení rovnic, nerovnic, soustav,...