Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 01. 2020 16:14
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Maximum value
If 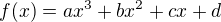 and
and  for
for ![kopírovat do textarea $x\in[-1,1]$](/mathtex/f7/f7b2009c5a761b979b09452fe39725b5.gif) . Then maximum value of
. Then maximum value of 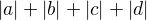 is
is
Offline
#2 03. 02. 2020 22:18 — Editoval jardofpr (03. 02. 2020 22:19)
Re: Maximum value
Offline
#3 10. 02. 2020 08:45
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Maximum value
Thanks ↑ jardofpr:
can you explain me in detail.
Offline
#4 10. 02. 2020 23:23
Re: Maximum value
Offline
#5 11. 02. 2020 15:17 — Editoval krakonoš (11. 02. 2020 21:33)
Re: Maximum value
↑ jardofpr:
Ahoj
Já jsem uvažovala podle podmínek 


Označím-li 
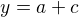
Dostávám podmínky

Z toho jsem vydedukovala, že 
Tedy 
Pak už vidím , že největší naději má situace, kdy a=k & c=-(k-1), (vzhledem k tomu ,že musí být  ) a snažím se zvolit co možná nejvyšší k, abych však dodržela podmínku omezenosti funkce podle zadání.Nevidím ale jinou možnost, než si vysledovat na intervalu <0;1> zda pro konkrétní k budou ještě spněny podmínky omezenosti .Taky mi připadá, že k=4 je to maximální , které by mohlo vyhovovat, když obecně zkoumám průběh funkce
) a snažím se zvolit co možná nejvyšší k, abych však dodržela podmínku omezenosti funkce podle zadání.Nevidím ale jinou možnost, než si vysledovat na intervalu <0;1> zda pro konkrétní k budou ještě spněny podmínky omezenosti .Taky mi připadá, že k=4 je to maximální , které by mohlo vyhovovat, když obecně zkoumám průběh funkce 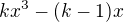 .
.
Když tuto funkci zderivuji a položím ji rovnu nule, dostanu body 
Pro k=4 je výraz roven +-1/2
Pro k=5 je roven +-0,51
Limitně je výraz roven +-0,577, pokud uvažuji kladné hodnoty, ta funkce je rostoucí.
Ta polovina pro k=4 je však klíčová, protože má být  , Tady už je vidět ,že k=5 už bude moc vysoké, tedy vyhovuje maximálně k=4.
, Tady už je vidět ,že k=5 už bude moc vysoké, tedy vyhovuje maximálně k=4.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#6 12. 02. 2020 13:52
Re: Maximum value
ahoj ↑ krakonoš:
pekny postup ale zda sa mi ze je dost problematicke sa vymotat z toho korektne tym smerom ze
uz sa uvazuje len polynom s neparnymi mocninami  .
.
|d|<= 1 sa mi nezda ako dostatocny argument na polozenie b=d=0
teda mozno za tym nejaky pevnejsi dovod mas len o nom nepises
Offline
 in as many points of the interval as many the coefficients of the polynomials are present
in as many points of the interval as many the coefficients of the polynomials are present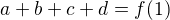
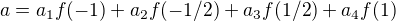


![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) usually reached
usually reached .
.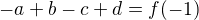
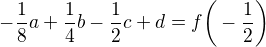
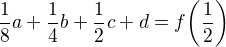

![kopírovat do textarea $a = \frac{2}{3}\big[f(1)-f(-1)+2f(-1/2) - 2f(1/2)\big]$](/mathtex/9e/9ea3af82fe9d4878a1f8c982577c02f7.gif)
![kopírovat do textarea $b = \frac{2}{3}\big[f(-1)+f(1) - f(-1/2)-f(1/2)\big]$](/mathtex/32/32ed0c8e5374c28849a0477ebaa23332.gif)
![kopírovat do textarea $c = \frac{1}{6}\big[f(-1)-f(1)+8f(1/2)-8f(-1/2)\big]$](/mathtex/0b/0b8ade65fd7bb160ce54770cd4dfc5cb.gif)
![kopírovat do textarea $d = \frac{1}{6}\big[4f(1/2)+4f(-1/2)-f(1)-f(-1)\big]$](/mathtex/fb/fbc68006e087183a9a2d0f0b04489fdb.gif)
 using
using 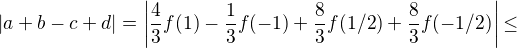
![kopírovat do textarea $\leq\frac{1}{3}\bigg[4|f(1)| + |f(-1)| +8|f(1/2)| + 8|f(-1/2)|\bigg]\leq 7$](/mathtex/3c/3ce6f01f24d04e037c9d6b31826d8ed5.gif) as
as 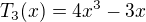 ,
,