Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extrémy funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 02. 2020 18:12
Extrémy funkce více proměnných
Ahoj,
řeším příklad a nevím, zda ho mám správně. Problém jsem měla s technikou, protože pokaždé mi to dávalo něco jiného
a nevím, co je to správné.
Spočítala jsem stacionární body, tj. body podezřelé z extrému. Vyšlo mi [0,0,3], [0,3,0], [3,0,0].
Hessova matice mi vyšla pro všechny body semidefinitní, a tedy nevíme nic.
Dále např. pro bod [3,0,0]
A) Volme x=t, y=1, z=2-t kde t náleží R
f(t) = t* (3-t)
pro t=2 má funkce maximum
B) Volme x=3-t, y=1, z=2+t kde t náleží v R
f(t) = (-t)* (3-t)
pro t= -2 má fce v bodě minimum.
Tedy v tomto bodě není lokální extrém. Analogicky pro ostatní body
Celkově funkce tedy nemá žádné lokální/globální extrémy?
Co se týká techniky:
Wolfram mi dával toto:
Mathematica mi dávala toto:
Co je tedy správně? A proč se to liší?
Offline
- (téma jako vyřešené označil(a) Pomeranc)
#2 29. 02. 2020 20:52 — Editoval surovec (29. 02. 2020 22:37)
Re: Extrémy funkce více proměnných
↑ Pomeranc:
Hoď na to Lagrangeovy multiplikátory, ty vedou rychle k výsledku...
Offline
#3 29. 02. 2020 21:38
Re: Extrémy funkce více proměnných
↑ surovec:
Já jsem se přes L. multiplikátory a nemohla jsem se dopočítat.
Proč tedy nevychází bod [1,1,1] z hledání stacionárních bodů?
Offline
#4 29. 02. 2020 22:18 — Editoval surovec (29. 02. 2020 22:19)
Re: Extrémy funkce více proměnných
↑ Pomeranc:
Protože to není stacionární bod. Je to extrém na vazební podmínce. Něco jako když vezmeš kousek paraboly na nějakém intervalu (to je ta vazba, to omezení). Může na něm být stacionární bod (vrchol paraboly), ale nemusí. Naopak ten extrém může být "na konci" toho intervalu, kde ta derivace vůbec nemusí být nulová. Tohle je totéž, jen o dvě dimenze výš.
Offline
#5 29. 02. 2020 22:36
Re: Extrémy funkce více proměnných
↑ surovec:
Možná to dává smysl. Jak se ještě dokáže, že v bodě [1,1,1] je maximum ?
Hessova matice mi tam nepomohla.
Offline
#6 29. 02. 2020 22:51 — Editoval surovec (29. 02. 2020 22:53)
Re: Extrémy funkce více proměnných
↑ Pomeranc:
Vyplývá to možná přímo z věty o Lagrangeových multiplikátorech, ale tím si takhle z fleku nejsem jistý. Takže bych zase zkoumal ("krychlové") okolí toho bodu (obdobně jako u těch sedlových bodů):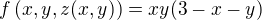
Krychlové okolí: 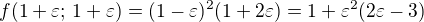 , což je evidentně menší než jedna (protože taková je hodnota tohoto maxima) pro jakékoliv
, což je evidentně menší než jedna (protože taková je hodnota tohoto maxima) pro jakékoliv  a tedy existuje okolí daného bodu (splňující vazební podmínku), na kterém má tento bod maximalní hodnotu.
a tedy existuje okolí daného bodu (splňující vazební podmínku), na kterém má tento bod maximalní hodnotu.
Offline
#7 29. 02. 2020 23:25
Re: Extrémy funkce více proměnných
↑ surovec:
Já bych řekla, že k tomu používáš jeden směr a nedokazuje to vyloženě to celé okolí.
Jako u sedlového bodu. Jenže problém je v tom, že bod je sedlový pokud najdeme alespoň jeden směr, kdy
v tom bodě bude minimum a dosazením 1+e, 1+e se to nezjistí.
Resp. když víš, že bod je sedlový, tak najít ty dva odlišné směry je celkem jednoduché, ale když je to min/max
tak to vyvrácení jednoho směru je těžší.
Možná zvolit  do x-sové souřadnice a
do x-sové souřadnice a  do y?
do y?
Offline
#8 29. 02. 2020 23:50 — Editoval Pomeranc (01. 03. 2020 00:17)
Re: Extrémy funkce více proměnných
↑ surovec:
Asi to mám. Nechám toto téma otevřené, kdyby se k tomu chtěl ještě někdo vyjádřit.
Děkuji za pomoc.
EDIT: stejně je divné, že Wolfram Alpha bod (1,1,1) ukazuje jak globální minimum, tak globální maximum.
Offline
#9 01. 03. 2020 00:17
Re: Extrémy funkce více proměnných
↑ Pomeranc:
Je zbytečné dávat tam ještě  , stačí vzít menší z nich a maximálně prostřídat znaménka.
, stačí vzít menší z nich a maximálně prostřídat znaménka.
Jak to myslíš, že používám jeden směr? Nikde nepíšu, že  je kladné, samozřejmě může být i záporné a ona nerovnost platí do všech směrů (++, --, +-, -+).
je kladné, samozřejmě může být i záporné a ona nerovnost platí do všech směrů (++, --, +-, -+).
Offline
#10 01. 03. 2020 00:24
Re: Extrémy funkce více proměnných
↑ surovec:
Ono je hned poznat, že dvojici +- ,-+ nemůžeš získat, protože e používáš jak pro x, tak pro y
a e nemůže být kladné a zároveň záporné. Zároveň do obou souřadnic přičítáš stejnou hodnotu.
Určitě nezkoumáš celé okolí. Domnívám se, že jdeš po přímce
x = 1+t
y= 1+t
z= 3-(1+t)-(1+t) kde t je v R
Offline
#12 01. 03. 2020 08:45 — Editoval surovec (01. 03. 2020 08:52)
Re: Extrémy funkce více proměnných
↑ Pomeranc:
Pravda, pravda, musí tam být různé hodnoty... Pak by ta nerovnost byla obtížnější na dokazování, ale na stejném principu...
Offline
#13 01. 03. 2020 11:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Extrémy funkce více proměnných
Zdravím,
obdobný problém související s WA jsme řešili v tématu, na doporučení kolegy Stýva podpora WA dostala oznámení a
WA v roce 2017 napsal(a):
We appreciate your feedback regarding Wolfram|Alpha. The issue you reported has been passed along to our development team for review. Thank you for helping us improve Wolfram|Alpha.
Best wishes,
The Wolfram|Alpha Team
www.wolframalpha.com
tak, pravda, nehořelo a stále nehoří :-)
↑ jarrro: metodu dosazování jsem použila zde, ale tím se mi podařil ztratit 1 kořen (pokud si vybavuji), ale kolega Rumburak to nejen napravil, ale také podrobně okomentoval v odkazovaném tématu, třeba také přispěje k problému ↑ Pomeranc:. Kolegovi Rumburakovi opět děkuji.
Offline
#15 01. 03. 2020 15:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Extrémy funkce více proměnných
↑ Pomeranc: také všem děkuji.
Podpoře WA jsem ovšem křivdila - nahlašovala jsem, že pro rovinu x+y+z=0 systém nachází 4 výsledky, tak to je opraveno, nachází jen 2 výsledky, to tedy opravovali.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Extrémy funkce více proměnných (TOTO TÉMA JE VYŘEŠENÉ)





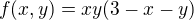 ).
).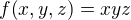 na rovine
na rovine 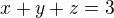 skúmať funkciu
skúmať funkciu  na
na 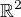 zrejme má
zrejme má  viazaný extrém práve vtedy keď
viazaný extrém práve vtedy keď  má globálny extrém a oba extrémy sú rovnakého typu
má globálny extrém a oba extrémy sú rovnakého typu