Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 03. 2020 14:01 — Editoval vanok (07. 03. 2020 14:04)
Re: Dělitelnost jedenácti
Ahoj ↑ kastanek:,
Najprv mala poznamka: tvoj zapis je nestandartny.
Bezne sa pise 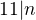 pre 11 deli cislo n. ( a nie
pre 11 deli cislo n. ( a nie  .
.
Inac ten tvoj dokaz iste dokazes aj sam urobit.
Staci konstatovat, ze 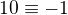
 . A potom to vyuzit. Tak mas
. A potom to vyuzit. Tak mas 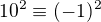 .
.  , cize.....pokracuj!
, cize.....pokracuj!
( pripominam, ze staci vediet 
 znamena, ze prirodzene a-b je delitelne 11-tymi ).
znamena, ze prirodzene a-b je delitelne 11-tymi ).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 07. 03. 2020 14:13 — Editoval jarrro (26. 05. 2023 19:41)
Re: Dělitelnost jedenácti
Nemáš opačne 11tku a číslo? Ak áno tak
[mathjax]\sum\limits_{i=0}^{n}{10^{i}{a_{i}}}=\sum\limits_{i=0}^{n}{\left(-1\right)^{i}a_{i}}+\sum\limits_{i=0}^{n}{\left(10^{i}-\left(-1\right)^{i}\right)a_{i}}
[/mathjax]
pričom každý koeficient je deliteľný
je deliteľný
MATH IS THE BEST!!!
Offline
#4 07. 03. 2020 14:15
Re: Dělitelnost jedenácti
↑ vanok:↑ kastanek:
Ahoj, ja si popravde moc nepamatuju, ze bychom 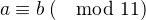 pouzivali na stredni.
pouzivali na stredni.
Zkusil bych se tomu vyhnout (ikdyz je to v podstate to same) a napsal bych si 
Z binomicke vety by to pak jiz melo byt lehke dokazat ;-)
Offline
#5 07. 03. 2020 14:29
Re: Dělitelnost jedenácti
Servus ↑ laszky:,
No mame podobne myslienky. A tiez aj binomicka veta sa na strednej skole, zda sa mi, sa uci len v pripade n=2 a n=3.
To asi preto sa to kriterium im dava bez dokazu....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 07. 03. 2020 15:03
Re: Dělitelnost jedenácti
↑ vanok:
Přiznám se, že tomu zápisu nerozumím ( znamená a-b? Proč tedy nepsat rovnou mínus?). Jinak binomická věta se většinou na středních školách bere (asi ne na uměleckých, zdravotních apod.).
znamená a-b? Proč tedy nepsat rovnou mínus?). Jinak binomická věta se většinou na středních školách bere (asi ne na uměleckých, zdravotních apod.).
↑ jarrro:
Krátké, elegantní. Díky!
↑ laszky:
No, "lehké dokázat"... :-)
Binomický rozvoj by byl v každém sčítanci té sumy a pak jednotlivé členy v jednotlivých rozvojích sčítat, to mi nepřipadá jednoduché. Nebo jsi to myslel nějak jednodušeji, co v tom teď nevidím?
Offline
#8 07. 03. 2020 15:19 — Editoval misaH (07. 03. 2020 15:26)
- misaH
- Příspěvky: 13431
Re: Dělitelnost jedenácti
Samozrejme, že sa to u nás na SŠ neučí...
Ináč ten znak v (trochu) iných súvislostiach znamená totožnosť (už ZŠ).
Offline
#9 07. 03. 2020 15:23
Re: Dělitelnost jedenácti
Ahoj ↑ kastanek:,
Len mala poznamka, s tym 
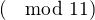 sa pracuje ako zo zvyskami po deleni 11, co sa tyka scitania a nasobenia. ( no skutocne sa to neuci v dnes na SS, i ked je to jednoduche).
sa pracuje ako zo zvyskami po deleni 11, co sa tyka scitania a nasobenia. ( no skutocne sa to neuci v dnes na SS, i ked je to jednoduche).
A v kazdom dokaze, z tych co su tu navrhnute, podobny problem. ( co sa tyka veci ucenych na strednej skole).
Napr. Aj v dokaze od kolegu ↑ jarrro: ( pozdravujem) ked pise  je delitelny
je delitelny  , je to nedokazane v jeho peknom prispevku.
, je to nedokazane v jeho peknom prispevku.
Ako vidis, je v takychto dokazoch tazko ostat v ramci strednej skoly.
No neskor na vysokoj skole to budes mat skutocne dokazane.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 07. 03. 2020 15:25
Re: Dělitelnost jedenácti
Offline
#11 07. 03. 2020 15:37 — Editoval kastanek (07. 03. 2020 15:40)
Re: Dělitelnost jedenácti
Offline
#12 07. 03. 2020 21:16 — Editoval jarrro (26. 05. 2023 19:56)
Re: Dělitelnost jedenácti
↑ vanok:vychádzal som z toho, že je to špeciálny prípad [mathjax]\left(a-b\right)\sum\limits_{k=0}^{n-1}{a^{n-1-k}b^{k}}
=\sum\limits_{k=0}^{n-1}{a^{n-k}b^k}-\sum\limits_{k=0}^{n-1}{a^{n-1-k}b^{k+1}}[/mathjax]
[mathjax]=\sum\limits_{k=0}^{n-1}{a^{n-k}b^k}-\sum\limits_{k=1}^{n}{a^{n-k}b^{k}}=[/mathjax]
[mathjax]=a^n+\left(\sum\limits_{k=1}^{n-1}{a^{n-k}b^k}\right)-\left(\sum\limits_{k=1}^{n-1}{a^{n-k}b^{k}}\right)-b^n=[/mathjax]
[mathjax]=a^n-b^n[/mathjax]
MATH IS THE BEST!!!
Offline
#13 07. 03. 2020 21:55 — Editoval vanok (07. 03. 2020 21:56)
Re: Dělitelnost jedenácti
Ahoj ↑ jarrro:,
Vsak ano.
No pre stredoskolaka to nie je to to najprirodzenejsie.
No ale aj praca mod 11 je tiez pre niektorych prirodzena a pre inych nie.
Co si myslis o pouziti tohto : 1 , 10 , 100 1000, ... sa pise mod 11
1; -1 , 1, -1,...
( aj na to musia cakat na vysoku skolu?)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 07. 03. 2020 23:09
Re: Dělitelnost jedenácti
↑ misaH:,
Skutocne?
A co meranie casu?
Napr.
3 h popoludni a 15 h.
Potom
Uhlove miery pre orientovane uhly.
A tiez su ine naznaky. Ako vlasnosti parnych a neparnych cisiel.
( niektori stredoskolak vedia pouzit aj situacie mod 3, i ked asi len na olympiadach....)
No tak ci tak, niektore dokazy treba nechat pre vysoku skolu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 07. 03. 2020 23:15 — Editoval Ferdish (07. 03. 2020 23:16)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Dělitelnost jedenácti
↑ vanok:
Ako náznaky áno, ale komplexnejšie podanie modula poťažmo kongurencií sa na strednej škole (gymnaziálneho charakteru) nepreberá.
Osobne si spomínam na operácie DIV a MOD aj to len čísla 10 v rámci hodín informatiky, tie som však mal iba v prvom ročníku, ďalej už nie (možno to viac mali vysvetlené spolužiaci, ktorí študovali so zameraním na informatiku).
A to bol prosím pekne rok 2005.
Offline
#17 07. 03. 2020 23:35
Re: Dělitelnost jedenácti
Pozdravujem ↑ Ferdish:,
Preto som napisal, ze niektore dokazy sa robia iba na vysokej skole.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 07. 03. 2020 23:56
Re: Dělitelnost jedenácti
↑ Ferdish:,
Ano, to je dobra poznamka. 👍
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

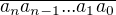 je označení pro (n+1)-ciferné číslo.
je označení pro (n+1)-ciferné číslo.