Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 04. 2020 11:17 — Editoval statistika_je_naj (07. 04. 2020 11:18)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Nezávislosť náhodných premenných
Ahojte, mam takuto definiciu nezavislych nahodnych premennych:
Nahodne premenne 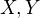 su nezavisle, ak
su nezavisle, ak  :
: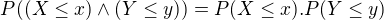
Chcel by som si overit ci ju chapem spravne. Mam priklad:
Uvažujme o roznych moznych poradiach narodeni chlapcov (B) a
dievcat (G) pri styroch porodoch. Teda:
BBBB BGBB GBBB GGBB
BBBG BGBG GBBG GGBG
BBGB BGGB GBGB GGGB
BBGG BGGG GBGG GGGG
Nech máme dve náhodné premenné:
X - počet dievčat
Y - počet chlapcov
Dostávamm:
x P(x)
0 1/16
1 4/16
2 6/16
3 4/16
4 1/16
y P(y)
0 1/16
1 4/16
2 6/16
3 4/16
4 1/16
Potom dostávam 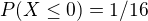 a tiez
a tiez 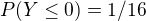 ale ako vypocitat vyraz
ale ako vypocitat vyraz 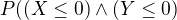 ? Nejako neviem co stym
? Nejako neviem co stym 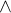 prosim poradte.
prosim poradte.
Offline
#3 07. 04. 2020 15:02
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
to viem aj ja .. ale co to znamena v praxi? mam tie pravdepodobnosti scitat alebo vynasobit?
Offline
#4 07. 04. 2020 15:07 Příspěvek uživatele surovec byl skryt uživatelem Stýv. Důvod: nesmysl
#5 07. 04. 2020 15:09
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
tak ale v tom pripade budu kazde dve nezavisle premenne X,Y zavisle nie? ked to staci len vynasobit ... vynasobim kazde dve a hotovo .. to mi nejako nesedi
Offline
#7 07. 04. 2020 15:23 — Editoval jarrro (07. 04. 2020 15:36)
Re: Nezávislosť náhodných premenných
↑ surovec:↑ statistika_je_naj:vo všeobecnosti ani sčítať ani vynásobiť.
Podobne ako si určil pravdepodobnosti pre X a Y tak určíš pravdepodobnosti pre dvojicu.
Tu konkrétne je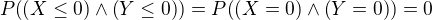 lebo nemôže byť v 4 pôrodoch súčasne nula chlapcov a nula dievčat (za predpokladu, že dieťa má práve jedno pohlavie)
lebo nemôže byť v 4 pôrodoch súčasne nula chlapcov a nula dievčat (za predpokladu, že dieťa má práve jedno pohlavie)
Na zistenie dvojrozmerného rozdelenia (diskrétneho) treba zistiť hodnoty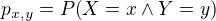 potom
potom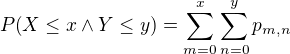
MATH IS THE BEST!!!
Offline
#8 07. 04. 2020 15:26
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
Stýv napsal(a):
Jaké dvě pravděpodobnosti? Máš tam jenom jednu pravděpodobnost.
myslel som P(X=x) to je prva pravdepodobnost a P(Y=y) to je druha pravdepodobnost.
Offline
#9 07. 04. 2020 15:33 — Editoval statistika_je_naj (07. 04. 2020 15:40)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
jarrro napsal(a):
↑ surovec:↑ statistika_je_naj:vo všeobecnosti ani sčítať ani vynásobiť.
Podobne ako si určil pravdepodobnosti pre X a Y tak určíš pravdepodobnosti pre dvojicu.
Tu konkrétne jelebo nemôže byť v 4 pôrodoch súčasne nula chlapcov a nula dievčat (za predpokladu, že dieťa má práve jedno pohlavie)
myslim, ze uz chapem .. takze napr.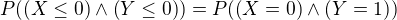 bude
bude 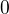 ? lebo neexistuje stvorica zlozena z chlapcov a dievcat ktora ma menej ako nula chlapcov a menej ako jedno dievca
? lebo neexistuje stvorica zlozena z chlapcov a dievcat ktora ma menej ako nula chlapcov a menej ako jedno dievca
Offline
#10 07. 04. 2020 15:42
Offline
#11 07. 04. 2020 15:44
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
hej uz som sa opravil a myslim ze bude platit: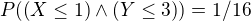
a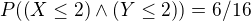
Offline
#12 07. 04. 2020 15:49 — Editoval statistika_je_naj (07. 04. 2020 15:51)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
Myslim ze ak to polozime do tabulky tak to bude takto:
x/y 0 1 2 3 4
0 0 0 0 0 1/16
1 0 0 0 1/16 5/16
2 0 0 6/16 4/16 10/16
3 0 1/16 4/16 14/16 15/16
4 1/16 5/16 10/16 15/16 16/16
a kedze plati ze napr. 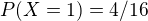 a
a 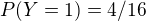 ale
ale  tak nahodne premenne X,Y nie su nezavisle.
tak nahodne premenne X,Y nie su nezavisle.
Offline
#14 07. 04. 2020 15:56
Offline
#15 07. 04. 2020 15:57
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Nezávislosť náhodných premenných
tak ok diki, myslim ze uz tomu rozumiem
Offline