Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vypocet kovariancie z tabuliek zadanych hodnot
#1 09. 04. 2020 01:52 — Editoval statistika_je_naj (09. 04. 2020 14:03)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
vypocet kovariancie z tabuliek zadanych hodnot
Ahojte, mam vypocitat kovariancu, pricom mam zadane tabulky hodnot pre nahodnu premennu  a
a  takto:
takto:
x p(x)
0 1/8
1 3/8
2 3/8
3 1/8
a
y p(y)
3 1/4
2 1/4
1 1/4
0 1/4
Postupoval som nasledovne:
podla vztahu ![kopírovat do textarea $cov(X,Y) = \sum_{x}^{}\sum_{y}^{}xy .p(x,y)=\frac{1}{n} \sum_{}^{} [(x-E(X)(y-E(Y)] $](/mathtex/c0/c0ed38c0f6477b3940d15486f492f7d8.gif)
najprv som vypocital hodnoty 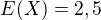 a
a 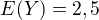 a potom som dosadil do vyssie uvedeneho vzorca:
a potom som dosadil do vyssie uvedeneho vzorca:![kopírovat do textarea $\frac{1}{4} [(0-\frac{3}{2}) (3-\frac{3}{2}) +(1-\frac{3}{2}) (2-\frac{3}{2}) + (2-\frac{3}{2}) (1-\frac{3}{2}) +(3-\frac{3}{2}) (0-\frac{3}{2} )]=-\frac{20}{8}$](/mathtex/9f/9f3f0f56f411f41e429e78924dbeac5e.gif)
Ten vzorec som nasiel tu: https://math.stackexchange.com/question … from-table
ale ked som skusil postupovat inac - cez vzorec 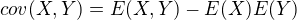
tak som si najprv vypocital 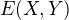 podla vztahu
podla vztahu 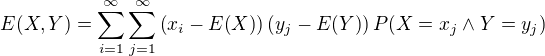
a dostal som:
 a dosadil do vztahu:
a dosadil do vztahu: 
Prosim vas, vobec mi to nevychadza, tri krat som to prepocital, hladam chybu a neviem ju najst. Neviem ktory postup je nespravny aj ked mam pocit ze ten druhy pretoze to nemam nasobit dvoma pravdepodobnostami ale len jednou, no neviem ako urobit z tych dvoch jednu pravdepodobnost. Budem vdacny za kazdu radu.
Offline
#4 09. 04. 2020 16:34
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: vypocet kovariancie z tabuliek zadanych hodnot
aha cize z len marginalnych sa to asi neda vypocitat vsak ..
Offline
#5 09. 04. 2020 17:06
Re: vypocet kovariancie z tabuliek zadanych hodnot
↑ statistika_je_naj:keď nevieš nič navyše (nezávislosť a podobne) tak nie
MATH IS THE BEST!!!
Offline
#6 09. 04. 2020 19:27
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: vypocet kovariancie z tabuliek zadanych hodnot
aha takze myslim ze uz chapem. Vztah  plati len pre nezavisle
plati len pre nezavisle 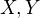
Offline
#7 10. 04. 2020 12:07
Re: vypocet kovariancie z tabuliek zadanych hodnot
↑ statistika_je_naj:
Rovnosť 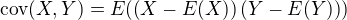 platí pre všetky a rovnosť
platí pre všetky a rovnosť iba pre nezávislé, ale v takom prípade je potom
iba pre nezávislé, ale v takom prípade je potom
MATH IS THE BEST!!!
Offline
#8 10. 04. 2020 14:00
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: vypocet kovariancie z tabuliek zadanych hodnot
tak ok, dakujem :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vypocet kovariancie z tabuliek zadanych hodnot