Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 02. 2021 18:10
logaritmicka rovnice
Ahoj. Řeším log. rovnici a nevim jak dál, ani jestli postupuji s korektními úpravami


 kladny vyraz pro
kladny vyraz pro 


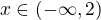
no takto mi to vyslo a navic asi pro kladny vyraz takze pro 
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
- (téma jako vyřešené označil(a) Meglun)
#2 22. 02. 2021 18:18 — Editoval Ferdish (22. 02. 2021 18:19)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: logaritmicka rovnice
Zdravím,
treba zvlášť ošetriť interval, na ktorom substituované [mathjax]u[/mathjax] nadobúda hodnoty medzi 0 a 1. Vtedy je totiž funkcia [mathjax]u^{x}[/mathjax] klesajúca.
Offline
#4 22. 02. 2021 19:25
Re: logaritmicka rovnice
↑ jarrro:
tak z teto upravy se mi podarilo asi vypocitat vysledek (-1,2).
Rozdelil interval logaritmu a soucinu a v (-1,2) jsou oba vyrazi kladne, takze kladne * kladne je vetsi jak 0
bohuzel jsem nepochopil jak dokoncit priklad, kdyz postupuji podle te substituce.
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#5 22. 02. 2021 20:03
Re: logaritmicka rovnice
↑ Meglun:
↑ Ferdish: ti to napsal. Musíš to rozdělit na dvě varianty
a)  , pak
, pak  a z toho jeden interval
a z toho jeden interval
b)  , pak
, pak  a druhý "interval"
a druhý "interval"
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 22. 02. 2021 20:06
Re: logaritmicka rovnice
↑ zdenek1:
rozumim jedne polovine a to jak sestavit intervaly...ale nevim jak na ty hodnoty 0 a 1 prijit sam
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#7 22. 02. 2021 21:22
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: logaritmicka rovnice
↑ Meglun:
To je jedna z vlastností exponenciálnej funkcie vzhľadom na hodnotu jej základu [mathjax]a[/mathjax].
Ak [mathjax]a>1[/mathjax] tak exp. fcia [mathjax]a^{x}[/mathjax] je rastúca a teda pre každé [mathjax]x_1<x_2[/mathjax] z jej definičného oboru platí [mathjax]a^{x_1}<a^{x_2}[/mathjax].
Ak [mathjax]a\in (0;1)[/mathjax] tak exp. fcia [mathjax]a^{x}[/mathjax] je klesajúca a pre každé [mathjax]x_1<x_2[/mathjax] z jej definičného oboru platí [mathjax]a^{x_1}>a^{x_2}[/mathjax].
Offline
#8 22. 02. 2021 21:44
Re: logaritmicka rovnice
↑ Ferdish:
no jo vlastne dekuji, neuvedomil jsem si to vubec
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline