Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Izomorfný vs neizomorfný
#1 01. 01. 2021 10:16 — Editoval fmfiain (01. 01. 2021 10:48)
Izomorfný vs neizomorfný
Dobrý deň,
mám takéto dve definície:
Izomorfné problémy - zhodná formálna štruktúra, iný obsah
Neizomorfné problémy - podobný obsah, odlišná štruktúra (je
potrebné využiť odlišné riešenia problému)
Príklad z praxe na izomorfné problémy: mám kvadratickú rovnicu a iba v nej zmením koeficienty a to tak, že prvý koeficient zostane nenulový.
Ale na príklad z praxe pre neizomorfné problémy nemôžem nájsť.
Pomôžete mi prosím.
Ďakujem za ochotu.
Offline
#2 01. 01. 2021 10:41 — Editoval fmfiain (01. 01. 2021 10:42)
Re: Izomorfný vs neizomorfný
Dobrý deň,
tak ma napadlo, že to neizomorfné môže byť:
Na začiatok máme lineárnu rovnicu s nenulovými koeficientami a prepíšeme ju na kvadratickú.
A to tak:
Koeficienty sa skoro (podobné) nezmenili ale riešenie sa mení.
Ďakujem za ochotu.
Offline
#3 01. 01. 2021 11:14
#4 01. 01. 2021 11:20
Re: Izomorfný vs neizomorfný
↑ vlado_bb:
Dobrý deň,
Problém - neželaná situácia, otázka na vyriešenie, dosiahnutie cieľa.
Offline
#5 01. 01. 2021 14:38 — Editoval vlado_bb (01. 01. 2021 14:38)
Re: Izomorfný vs neizomorfný
↑ fmfiain:To nie su korektne definicie. Ale ak chces priklad neizomorfnych problemov pri intuitivnom chapani tohoto pojmu tak tu su:
Problem 1: najst riesenie rovnice 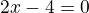
Problem 2: zostrojit trojuholnik, ak pozname jeho strany.
Offline
#6 02. 01. 2021 10:19 — Editoval fmfiain (02. 01. 2021 10:30)
Re: Izomorfný vs neizomorfný
↑ vlado_bb:
Dobrý deň,
tie tri strany trojuholníka sú vlastne tri priamky s premennými x a y?
Jedná sa o to, že máme rovnaký obsah, čiže 2D priestor a odlišnú štruktúru, čiže priamku a trojuholník?
A k tomu izomorfnému problému, mám ten príklad z praxe v poriadku? Ja som to totiž riešil intuitívne.
Na tie izomorfné by intuitívne mohlo byť, že zoberieme dva odlišné obsahy, napríklad 2D a 3D priestor a rovnakú štruktúru, napríklad priamku.
Ďakujem za odpoveď.
Offline
#7 23. 09. 2021 12:58
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Izomorfný vs neizomorfný
↑ fmfiain:
Pokud jsem správně pochopil, jde o využití izomorfismu při řešení nějakého problému. Změna koeficientů kvadratické rovnice není o izomorfismu, to jsou jenom dvě konkretizace obecného vzorečku. Izomorfismus lze použít zcela běžně např. v geometrii při řešení konstrukční úlohy pravítkem a kružítkem. Zadání vyjádřit analyticky v souřadnicích (bod = uspořádaná dvojice čísel), konstrukci spočítat a výsledek pak sestrojit pravítkem a kružítkem.
Na jedné straně je P-K geometrie (pravítko - kružítko), na druhé analytická geometrie.
I když - přesně řečeno - tady nejde o izomorfizmus, ale pouze o monomorfizmus P-K ---> analytická. Všechny P-K úlohy lze řešit analyticky, ale ne naopak (například kvadratura kruhu je v P-K geometrii neřešitelná, analyticky velmi snadno:-)
"Neizomorfizmus" je velmi mlhavý pojem. Jsou to zřejmě všechny struktury, které nejsou izomorfní, což jsou ovšem i struktury, které nemají prakticky nic společného. Něco takového bude asi k ničemu...
Budoucnost patří aluminiu.
Offline
#8 23. 09. 2021 13:04
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Izomorfný vs neizomorfný
↑ fmfiain:
Na izomorfismus mě napadá krásný příklad, ale chtělo by to sem dát obrázek a to nevím, jak. Dřív mi to nějak šlo, teď už to z neznámého důvodu nějak nejde...
Budoucnost patří aluminiu.
Offline
#9 23. 09. 2021 15:12
Re: Izomorfný vs neizomorfný
↑ Eratosthenes:
Ahoj, až na rok zadarmo uchovajú obrázok
Tu
https://ctrlv.cz
Offline
#10 23. 09. 2021 16:59
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Izomorfný vs neizomorfný
↑ pietro:
Zajímavé - použiju. I když byly doby, kdy se ctrl-v dalo použít přímo tady a obrázek byl přímo v příspěvku :-)
Budoucnost patří aluminiu.
Offline
#11 23. 09. 2021 17:18
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Izomorfný vs neizomorfný
↑ fmfiain:
Takže: Tři shodné čtverce - viz obrázek
https://ctrlv.cz/qTR6
Úkolem je najít součet velikostí úhlů
Samozřejmě je
ale kdo by si pamatoval součtové vzorce pro arctg? A hledat to na internetu je zbabělost :-) Jde to i jinak....
Budoucnost patří aluminiu.
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Izomorfný vs neizomorfný
