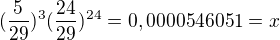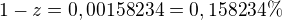Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2020 14:13
pravděpodobnost
Dobrý den,
Mám zajímavý příklad, přiložím řešení a prosím o jeho opravu.
Zadání:
Ve třídě je 27 holek, bereme že každý měsíc má 29 dní, každá holka má každý měsíc menstruaci trvající 5 dní.
Jaká je šance že alespoň jednou za měsíc nastane den kdy mají právě tři holky menstruaci.
mé řešení:
Offline
#2 30. 04. 2020 01:47 — Editoval nejsem_tonda (30. 04. 2020 01:48)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: pravděpodobnost
↑ Pozitron:
Ahoj,
pravdepodobnost je zaludna.
Nespravnost tve uvahy se pokusim ukazat treba takto:
Vezmeme si jednu holku, treba Tamaru. Jaka je pravdepodobnost, ze Tamara dnes nema menstruaci? 24/29.
Jaka je pravdepodobnost, ze Tamara nema menstruaci zadny den v mesici?
Pritom ale logickou uvahou je uplne nesmyslne, aby ta pravdepodobnost byla vetsi nez 0. Tamara preci nekdy v mesici mestruaci urcite dostane.
Problem je napriklad v tom, ze predpokladame, ze jednotlive dny jsou na sobe zcela nezavisle. Jako kdyby si Tamara kazdy den hodila minci, na ktere pada jedna strana s pnosti 5/29 a druha s pnosti 24/29. Ve skutecnosti jsou na sobe jednotlive dny zavisle. Napriklad pokud Tamara nemela menstruaci prvnich 20 dni, pak pravdepodobnost, ze 21. ji mit bude, je uz pomerne velka, rozhodne vetsi nez 5/29. Kdyby menstruaci nemela prvnich 24 dni, tak uz je dokonce jistota, ze 25. den ji mit bude.
Offline
#3 19. 01. 2022 10:35 — Editoval neutr (19. 01. 2022 16:35)
Re: pravděpodobnost
Pozitron napsal(a):
Dobrý den,
Mám zajímavý příklad, přiložím řešení a prosím o jeho opravu.
Zadání:
Ve třídě je 27 holek, bereme že každý měsíc má 29 dní, každá holka má každý měsíc menstruaci trvající 5 dní.
Jaká je šance že alespoň jednou za měsíc nastane den kdy mají právě tři holky menstruaci.
mé řešení:
Tato úloha je nad možnosti středoškolské matematiky. Je nutné udělat mnoho výpočtů. Stručně vysvětlím problém :
A) Problém má základ v tom, že můžeme požadovat pouze 3 dívky s menstruací (jak vyplývá ze zadání), nikoliv více. Ve skutečnosti se dvě dívky mohou v rámci menstruace potkat až na intervalu 9 dní (například poslední den jedné dívky a první den druhé dívky). Konkrétně souběh je možný od 5-ti dní až do 9-ti dní.
B) Celkově je možné uvažovat : že se v jeden den potká menstruace u všech děvčat naráz.
Na druhém konci je extrém, kdy se nepotká menstruace u žádné dvojice dívek. Tento extrém je ale vyloužen biologicky, jinak by to bylo nejméně 27 x 5 = 135 dní. Pokud jde o 29 dní, pak 29/5 = cca 6 dívek. Slovy v intervalu 29 může nastat 1 případ z mnoha, kdy se u žádné ze šesti dívek menstruace nepotká.
C) Jde - li o výpočet všech různých možností, tedy se zadáním souběh menstruací včetně 3 a více dívek je nutno použít rozšířené hypergeometrické rozdělění, jehož základem je "partition" (správně Partitio Numerorum). Při postupu je nutno použít PN(27) i PN(29). PN(27) má 3010 řádků a PN(29) už 4565 řádků.
ad A) : Jen orientačně : Počet různých trojic z celku 27 = 2925
ad B) : Pokud 29 dní rozdělíme po pěti na 6 dílů například (4,5,5,5,5,5) dostaneme 331 vhodných řádků. Pokud rozdělíme na 7 dílů, například (2,5,5,5,5,5,2) dostaneme 364 vhodných řádků.
ad C) : V případě souběhu menstruací do jediného dne nenastane souběh ve 14-ti z 3010 možných případů = 2,92 %. Pravděpodobnost, že bude některý den menstruovat 3 a více dívek je veliká 97% a to je ve skutečnosti jen úvaha pro jediný den, ale menstruace trvá 5 dní.
Výpočty a ukázky z čeho vycházet na vyžádání připravím v sešitě Excel
PS
Špatně jsem si zapamatoval počet dívek ze zadání, není tam 24 dívek, ale 27. Celkem na tom nezáleží, protože čísla mimo ad A) byla správně. Nyní jsem to opravil.
Offline
#5 19. 01. 2022 17:57 — Editoval neutr (19. 01. 2022 17:59)
Re: pravděpodobnost
pro Brano
Celkem nechápu jak to myslíte.
Brano napsal(a):
toto je typ prikladu, kde sa oplati to nasimulovat a byt spokojny s "experimentalnym" vysledkom
Já jsem měl na mysli těchto 14 uspořádání bez trojice z celku 3010. Rozložení do 29 dnů je shodné, jen by tam byly v každém řádku dvě nuly navíc.
2,2,2,2,2,2,2,2,2,2,2,2,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0
2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0
2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0
2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0
2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0
2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0
2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0
2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
Pozitron napsal(a):
Jaká je šance že alespoň jednou za měsíc nastane den kdy mají právě tři holky menstruaci
Takových případů nastane dost a je i dost případů kdy se vyskytnou 2 a více trojic (maximálně 9). Ještě by se mělo upřesnit, zda se může vyskytovat i větší k-tice, nežli trojice, ale i takových řádků, kde je jediná trojice a ostatní k-tice jsou menší (dvojice a jednice) je dost.
1 trojice se vyskytuje v 783 řádcích (26,01 %)
2 trojice se vyskytují v 407 řádcích
3 trojice se vyskytují v 209 řádcích
4 trojice se vyskytují v 99 řádcích
5 trojic se vyskytuje v 47 řádcích
6 trojic se vyskytuje v 19 řádcích
7 trojic se vyskytuje v 8 řádcích
8 trojic se vyskytuje v 2 řádcích
9 trojic se vyskytuje v 1 řádku
Celkem se jedná o 1575 případů z celku 3010 = 52,33 %
Jak vidíte je to složitější. Autor nepředpokládal ani zdaleka, že by alespoň 1 trojice měla pravděpodobnost 26%. Pokud by existovalo upřesnění ve smyslu "největší k-tice a navíc jediná (trojice)" bylo by číslo také jiné celkem 13 řádků :
3,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,2,2,2,2,2,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0
3,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0
3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0
3,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0
3,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0
3,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0
3,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0
3,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0
Offline
#6 19. 01. 2022 20:27 — Editoval Brano (19. 01. 2022 20:33)
Re: pravděpodobnost
neutr napsal(a):
pro Brano
Celkem nechápu jak to myslíte.Brano napsal(a):
toto je typ prikladu, kde sa oplati to nasimulovat a byt spokojny s "experimentalnym" vysledkom
mal som na mysli povodnu ulohu.
jeden pokus je, ze nasimulujeme 27 nahodnych zaciatkov menstruacie v 29 dnovom mesiaci a zistime ci sa tam nachadza den s prave tromi subeznymi
cele to zopakujeme povedzme 100 000 krat a nasimulovany odhad pravdepodobnosti je pocet uspesnych pokusov deleno 100 000 ... standardna Monte Carlo metoda
PS: plne suhlasim s tym ze autorovo riesenie je uplne mimo; aj keby sa mohlo stat, ze numericky by sa podobalo na skutocnu hodnotu tej pravdepodobnosti ..
Offline
#7 21. 01. 2022 18:19
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: pravděpodobnost
↑ Pozitron:
Ahoj. "Jaká je šance" znamená přesně co? Jaká je pravděpdoobnost? Nebo zda to vůbec může nastat?.....
"Máte úhel beta." "No to nemám."
Offline