Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 06. 2018 04:38
Složitější kvadratická rovnice s parametrem
Chtěl bych poprosit, jestli by mi tu někdo nerozepsal řešení této rovnice. Já sice umím řešit podobný typ rovnic, problém je, že tahle mi přijde složitější => především kvůli této části p(x^2 − 6x + 8) , rád bych věděl jak v takovém případě postupovat
Určete hodnoty reálného parametru p tak aby rovnice měla jedno řešení: 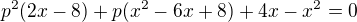
(chápu, že diskriminant musí být 0, aby měla jen jedno řešení)
Offline
#2 02. 06. 2018 06:26 — Editoval zdenek1 (18. 06. 2018 09:31)
Re: Složitější kvadratická rovnice s parametrem
↑ Ikaruss:
otevřít závorky
a "přerovnat" do klasického tvru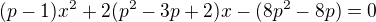
a pozor, nestačí podmínka pro diskriminant, musíš taky zkontrolovat, co se stane, když  , protože pak to není kvadratická rovnice.
, protože pak to není kvadratická rovnice.
edit
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 18. 06. 2018 02:47 — Editoval Ikaruss (18. 06. 2018 02:53)
Re: Složitější kvadratická rovnice s parametrem
Trochu se zpožděním, ale ve skutečnosti mne především zajímalo, jak postupuji dál, po té co si to takhle přerovnám:) Já předpokládám, že stačí aby p = 0 a potom ta rovnice bude mít zrovna jedno řešení, což je zadání u této rovnice...
Offline
#4 18. 06. 2018 06:52
Re: Složitější kvadratická rovnice s parametrem
↑ Ikaruss:
a) máš určit hodnoty, čímž se myslí všechny hodnoty.
b) 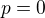 dává dvě řešení
dává dvě řešení  a
a 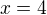
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 05. 04. 2022 09:38 — Editoval JakubJeh (05. 04. 2022 09:40)
Re: Složitější kvadratická rovnice s parametrem
↑ zdenek1: Ahoj, nerozumim navrhnu tohoto reseni. Pokud si za p dosadim 0 tak prece nemusim delat zadne roznasobovani(otevreni zavorek). Vyjde mi ta sama kvadraticka rovnice -x^2 + 4x a dostanu dva koreny 0 a 4. Navic jak vim ze toto reseni je jedine a plati pouze pro p=0 ? Jaky je tedy spravny postup u tohoto typu rovnice?
Dekuji
Kuba
Offline
#8 05. 04. 2022 10:53 — Editoval Honzc (05. 04. 2022 10:54)
Re: Složitější kvadratická rovnice s parametrem
↑ JakubJeh:
V zadání je přece napsáno pro jaká p má uvedená rovnice ... jedno řešení (to je x=něco)
To tvoje řešení pro p=0 dává 2 řešení x1=0 a x2=4 a to jistě uznáš, že není jenom jedno řešení.
Správný postup je:
rovnici upravíme na
[mathjax](p-1)x^{2}+2(p-1)(p-2)x-8p(p-1)=0[/mathjax]
Pro [mathjax]p\ne 1[/mathjax]
dostaneme
[mathjax]x^{2}+2(p-2)x-8p=0[/mathjax]
Aby rovnice měla jedno řešení pak [mathjax]D=0[/mathjax]
[mathjax]D=(p-2)^{2}+8p=0[/mathjax]
a tedy
[mathjax](p+2)^{2}=0\Rightarrow p=-2[/mathjax]
což je řešením
Offline

 ?
?