Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 10. 2009 15:44
mocniny a odmocniny
Ahoj, omlouvám se, že zas otravuju, ale nebojte, jen do konce týdne :-). Mám tu 4. okruh Odkaz, většinu už mám vypočítanou, ale potřebovala bych to tak trochu zkontrolovat, protože si nejsem zrovna jistá ve svejch postupech. A přeci jenom je tu ještě pár příkladů, se kterýma si nevim rady a to 1ac, 2a a 6a a byla bych vděčná za postup :-).
Díky moc :-)




Offline
#2 30. 10. 2009 15:46
Re: mocniny a odmocniny
↑ 007Misak:
ak nevies postup tak napis co ti vyslo alebo kde si skoncila, najdeme chybu
Offline
#4 30. 10. 2009 16:09 — Editoval Tychi (30. 10. 2009 16:25)
Re: mocniny a odmocniny
6b máš správně
5b je také správně
5a jsem ti počítala tady, příspěvek 5, i když tam se to jmenovalo 4c...
4b je správně
.
.
.
1b je správně
1a tam se zbavíš absolutních hodnot jednoduše, první rozdíl v absolutní hodnotě je kladný, takže abs. hodnotu můžeš vynechat, druhý je záporný, takže změníš znaménko před ní a počítáš a ní dál jako se závorkou.
Zbytek nechám na někom jiném.
Vesmír má čas.
Offline
#7 05. 11. 2009 20:32 — Editoval Honza Matika (05. 11. 2009 20:34)
#10 06. 11. 2009 16:23 — Editoval FailED (27. 04. 2010 15:51)
Re: mocniny a odmocniny
↑ jarad4848: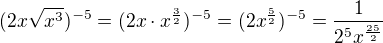
↑ Zdeňka:
Cemu nerozumis? Nejdriv si uprav ten podil, zacni tim, ze upravis jmenovatele, deleni zlomkem je to same jako nasobeni jeho prevracenou hodnotou.
Offline

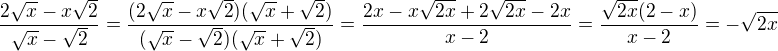



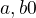
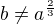
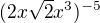

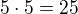 asi jen překlep
asi jen překlep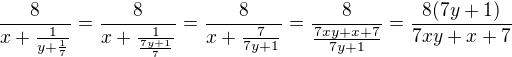
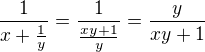
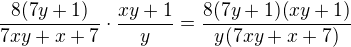
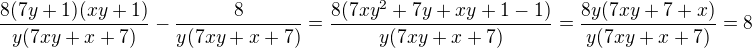
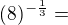 A to už zvládneš.
A to už zvládneš.