Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 11. 2009 13:45
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Mocniny s racionálním exponentem
Vytrženo z jiného tématu:
hofmanova.darina napsal(a):
Ahoj tady Darča,
potřebovala bych poradit s počítáním mocnin s racionálním exponentem.
Příklad:x1/3.x2/3
------------
x1/2
nějak nemůžu přijít na to jak to vypočítat
díky za pomoc
Cheop napsal(a):
- při násobení se mocniny sčítají při dělení se odčítají tj:
2+2=4
Offline
#10 07. 11. 2009 23:25 — Editoval jelena (08. 11. 2009 09:42)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Mocniny s racionálním exponentem
↑ Ivana:
Ivano, zdravím srdečně i přes jiné komunikační prostředky :-)
Možna jen takové doporučení - navrhla bych použití substituce  nebo i substituce
nebo i substituce 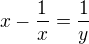 a
a  . Hodí se?
. Hodí se?
ve Tvé úpravě v kroku 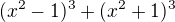 je trochu mene pracne pouzit vzorec
je trochu mene pracne pouzit vzorec 
Možná se bude hodit něco podobného: http://forum.matweb.cz/viewtopic.php?pid=69852#p69852
Zdravím u vás :-)
EDIT: doplnila jsem ještě jednu substituci - za celou závorku.
Offline
#12 08. 11. 2009 09:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Mocniny s racionálním exponentem
↑ Ivana:
Zdravím, Ivano,
pravě jsem doplňovala i další možnou substituci. Naprosto souhlasím, že je to věc názoru, v mém případě použití substituce je vyvoláno hlavně moji lenosti a také, že při práci s mocninami bych nasekala určitě hodně chyb.
Hezký den :-)
Offline
#13 08. 11. 2009 09:57
- marnes

- Příspěvky: 11227
Re: Mocniny s racionálním exponentem
↑ jelena:↑ Ivana: Zdravím obě:-)
Příklad je to hezký, problém je v tom, že autor vůbec nezná základní práci se zlomky (své příspěvky přes noc vymazal )a o dalších úpravách ani nemluvím a hned chce tyto "lepší příklady".
Jo. A na začátku vás zdravím.
Offline
#15 08. 11. 2009 11:43
- marnes

- Příspěvky: 11227
Re: Mocniny s racionálním exponentem
↑ jelena:
Nenene, to nebylo vůbec na tebe. Mě se nápad se substitucí líbí. Já tím chtěl jen říct, že by se autor tohoto příkladu měl nejdříve soustředit na jednodušší příklady, když nezná elementární úpravy, protože pak to jen opíše a nic neumí.
Jo. A na začátku vás zdravím.
Offline
#16 09. 11. 2009 16:34
Re: Mocniny s racionálním exponentem
↑ marnes:Zdravím Tě kolego, :-)
jen malý dodatek ... ze svých zkušeností, vím, že těch , co jenom opisují je daleko více než těch, kteří u toho počítání i přemýšlejí.... Škoda , že :-(
Jedna krát jedna je " tisíckrát " jedna :-)
Offline

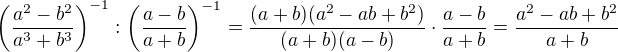
 druha
druha 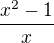 jmenovatel
jmenovatel 
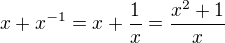
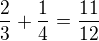 spolecny jmenovatel je
spolecny jmenovatel je 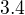 a citatel je
a citatel je 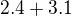



.jpg)