Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica na k-tu sa rovná nule (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 08. 2021 20:07
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Matica na k-tu sa rovná nule
Využívajúc trik z predošlej témy (https://forum.matweb.cz/viewtopic.php?id=111364) sa snažím nájsť všeobecné riešenie pre problém:
Je pravda, že ak 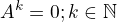 , tak
, tak  je invertibilné?
je invertibilné?
Tento problém som si najprv vyjadril v maticiach - ak je tvrdenie hore pravda, tak potom existuje X také, že: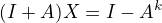
Manuálnym výpočtom som si pre n=1,2,3,4 overil, že 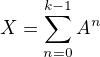 , ale je to pravda pre všetky n? Ak áno, ako sa k tomu dostanem z prvej rovnice?
, ale je to pravda pre všetky n? Ak áno, ako sa k tomu dostanem z prvej rovnice?
Ako si vôbec izolujem X, keď násobenie matíc nie je komutatívne a to X mi vždy nejako zostane medzi zvyšnými dvoma členmi a ich inverznými formami.
Offline
- (téma jako vyřešené označil(a) sjaustirni)
#2 11. 08. 2021 23:35 — Editoval Brano (11. 08. 2021 23:41)
Re: Matica na k-tu sa rovná nule
jednoducho sa da overit, ze pre lubovolnu stvorcovu maticu  plati
plati
(to je presne ta ista uvaha ako scitanie geometrickeho radu)
a v pripade, ze  potom je
potom je  z definicie inverzna k
z definicie inverzna k 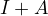 , takze odpoved na tvoju otazku je ano, len si daj pozor na znamienka
, takze odpoved na tvoju otazku je ano, len si daj pozor na znamienka
da sa to aj vseobecnejsie, konkretne mozes podobnym sposobom ukazat, ze 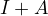 ma inverznu maticu
ma inverznu maticu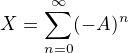
len musis zabezpecit aby ten rad konvergoval; co plati napriklad ak  pre nejake
pre nejake  ; alebo ina podmienka moze byt
; alebo ina podmienka moze byt  (operatorova norma)
(operatorova norma)
Offline
#3 12. 08. 2021 15:56
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Re: Matica na k-tu sa rovná nule
Jj, pri prepise som zabudol na znamienko, myslel som samozrejme 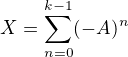
A áno, inšprioval som na to z geometrického radu (dík H20 za tvoj post :D), ale vyjde mi to len ak sa tvárim, že členy sú skaláry. Nejako sa k tomu neviem dostať cez matice.
Konkrétne, prečo platí  ? Násobenie matíc nie je komutatívne, takže predpokladám, že mi uniká nejaká vlastnosť tejto dvojice, či?
? Násobenie matíc nie je komutatívne, takže predpokladám, že mi uniká nejaká vlastnosť tejto dvojice, či?
Offline
#4 12. 08. 2021 18:42
Re: Matica na k-tu sa rovná nule
Ahoj ↑ sjaustirni:,
Mala poznamka.
No ako pises v tvojom predoslom prispevku, X je «polynom v A » (prvy riadok) tak v tomto pripade mas autonaticky komutativitu.
( inac, take matice ako A sa volaju nilpotentne. Nieco analogicke najdes tu : https://forum.matweb.cz/viewtopic.php?id=108958 )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 12. 08. 2021 19:33 — Editoval sjaustirni (12. 08. 2021 19:33)
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Re: Matica na k-tu sa rovná nule
Nilpotentné matice som nepoznal a wiki stránka o nilpotentných maticiach dokonca rozoberá problém (I+A) z tejto témy.
Mnohokrát vďaka Braňo za opravu a nasmerovanie a vánok, za tvoj komentár.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica na k-tu sa rovná nule (TOTO TÉMA JE VYŘEŠENÉ)
