Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 10. 2011 13:25 — Editoval ShadyDrob_cz (27. 10. 2011 13:29)
- ShadyDrob_cz

- Příspěvky: 59
- Reputace: 0
Limita s gon. funkcí - 1
Prosím o radu jak jít na výpočet této limity:
Poznámka: někdo mi poradil ať použiji L'Hospitalovo pravidlo, bohužel to nejspíš nemužu použít zvhledem k tomu, že ve škole jsme ještě něbrali derivace a pravidlo samotné
Díky
Offline
#2 27. 10. 2011 13:53 — Editoval vanok (27. 10. 2011 13:54)
Re: Limita s gon. funkcí - 1
↑ ShadyDrob_cz:
Tu moze pomoct 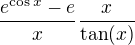
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 31. 10. 2011 18:25 — Editoval ShadyDrob_cz (31. 10. 2011 18:25)
- ShadyDrob_cz

- Příspěvky: 59
- Reputace: 0
Re: Limita s gon. funkcí - 1
Přepokládám, že zde by asi bylo nejlepší ten prvni zlomek dostat do tvaru , bohužel nějak nevidim co s tim dál :/
Offline
#4 31. 10. 2011 18:27 — Editoval halogan (31. 10. 2011 18:32)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita s gon. funkcí - 1
1) Vytkni e v čitateli. A to pak vytkni úplně ven.
2) Jmenovatele "transformuj" na  pomocí návodu od ↑ vanok:. (Ono to není zas tak moc nutné, ale pomůže to trochu. I když... ono to ve finále bude možná i složitější, jak tak nad tim přemýšlim. Možná má kolega nějaký jiný plán, já bych tam ten tangens nechal, bude se hodit.)
pomocí návodu od ↑ vanok:. (Ono to není zas tak moc nutné, ale pomůže to trochu. I když... ono to ve finále bude možná i složitější, jak tak nad tim přemýšlim. Možná má kolega nějaký jiný plán, já bych tam ten tangens nechal, bude se hodit.)
3) Rozšiř výrazem v exponentu eulerova čísla v čitateli.
Jeden zlomek ti vypadne, ten druhý rychle dopočítáš.
Offline
#5 31. 10. 2011 19:09 — Editoval vanok (31. 10. 2011 19:13)
Re: Limita s gon. funkcí - 1
↑ ShadyDrob_cz:↑ halogan:
Ano to je dobra pomoc z tym e
Co sa tyka tangentu moze sa to napriklad upravit takto:
(ak nevies co sa deje z 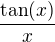 v okoli nuly )
v okoli nuly )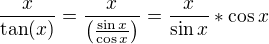
Staci ti to?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 31. 10. 2011 19:14
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita s gon. funkcí - 1
↑ vanok:
Já vím moc dobře, co se děje s tanx/x v okolí nuly :-) Jen nevidím důvod vkládat do původní limity  , když stejně budeme potřebovat jen
, když stejně budeme potřebovat jen 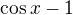 , které se nám po rozšíření zkrátí právě s částí té tangenty.
, které se nám po rozšíření zkrátí právě s částí té tangenty.
Kdybychom tu tangentu vyhodili ven přes tvůj návrh, tak musíme využít další limity (např. sinx/x) a aritmetiky a tak dál. To mi přijde jako moc práce navíc.
Offline
#7 31. 10. 2011 19:44
Re: Limita s gon. funkcí - 1
↑ halogan:
ano mas pravdu....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 31. 10. 2011 21:33 — Editoval ShadyDrob_cz (31. 10. 2011 21:39)
- ShadyDrob_cz

- Příspěvky: 59
- Reputace: 0
Re: Limita s gon. funkcí - 1
Je možné že to vyšlo -e?
Offline
#9 31. 10. 2011 22:01
Re: Limita s gon. funkcí - 1
↑ ShadyDrob_cz:
Mne vysla 0. A pouzil som metodu equivalentov. Ak chces dam ti rychly postup, ale sa zda ze tato metoda sa neuci ani v Cz a ani na Sk.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 31. 10. 2011 22:21
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita s gon. funkcí - 1
Nulu potvrzuji a dodávám pomocný postup
1) Vytknout e v čitateli.
2) Rozšířit zlomkem, kde čitatel i jmenovatel je 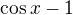 .
.
3) Přes aritmetiku rozdělit na dvě limity a jednu přes limitu složené funkce dopočítat (vede to na to [e^x -1]/x).
4) Vytknout -1 z 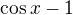 , rozšířit
, rozšířit 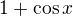 , a nahoře dostaneš
, a nahoře dostaneš 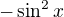
5) Dolní 1 + sin x můžeš přes aritmetiku vyhodit, bude to jednička.
6) Zkrátit jeden ze sínů nahoře se sínem z tangenty
... a už jsme skoro tam.
Offline
#11 31. 10. 2011 22:51 — Editoval vanok (31. 10. 2011 22:52)
Re: Limita s gon. funkcí - 1
Metode equivalentov v 0 je rychla, ak sa poznaju zakladne equivalencie a ich vlasnosti.
Mame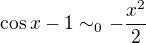
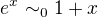
co da 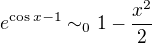
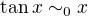
Co nam da
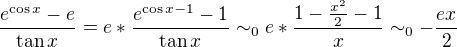
Akoze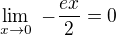
tak aj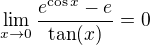
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 31. 10. 2011 23:12
- ShadyDrob_cz

- Příspěvky: 59
- Reputace: 0
Re: Limita s gon. funkcí - 1
Aha, perfektní, zkusim toto jeste prozkoumat. Mnohokrát díky za pomoc.
Offline
#13 01. 11. 2011 13:04
Re: Limita s gon. funkcí - 1
↑ ShadyDrob_cz:
Dobre, ale akoze ste sa neucili "moju" metodu musis vediet dokazat vsetko co pouzijes.
Ale aj dokaz od kolegu mozes pouzit( dat strucne vysvetlenia iba)", lebo vyuziva len co ste sa ucili... a goniometricke funkcie to je asi "krasa" elementarnej matematiky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline