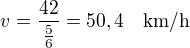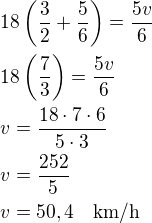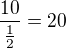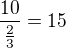Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#101 04. 01. 2010 18:51
Re: slovní úlohy o pohybu
Chrpa napsal(a):
↑↑ Honzas:
Celková doba jízdy cyklisty je 1,5 + 5/6 =7/3 hodiny
Za tu dobu ujel rychlostí 18 km/h vzdálenost 18*7/3 = 42 km.
Automobil musel ujet tu samou vzdálenost (nakonec ho dojel) tj. ujel taky 42 km. Potřeboval na to 50 minut = 5/6 hodiny
Jeho rychlost je:
Rovnicí by to bylo:
Lze to řešit pomocí rovnice s jednou , dvěma neznámímy ?
Offline
#102 04. 01. 2010 19:00 — Editoval Chrpa (04. 01. 2010 19:11)
Re: slovní úlohy o pohybu
↑↑ Honzas:
Označme:
x - počet krabic, které jsou po 6 ks
41 - x - počet krabic, které jsou po 4 ks.
Pak platí:
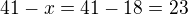
A) 4 sklenice bude obsahovat 23 krabic
B 6 sklenic bude obsahovat 18 krabic
Řešení pomocí 2 rovnic o 2 neznámých:
x - počet krabic po 4 ks
y - počet krabic po 6 ks
Rovnice:
1) 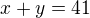
2)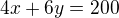 první rovnici vynásobím (-4) a sečtu s druhou) tj:
první rovnici vynásobím (-4) a sečtu s druhou) tj: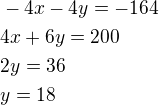

Výsledek je stejný.
Offline
#103 21. 06. 2012 16:20
#104 26. 06. 2012 21:19
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 242
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: slovní úlohy o pohybu
Pre tych ktorych nebavi pocitat stale rovnaky priklad o cyklistovi:
http://www.hackmath.net/sk/slovne-ulohy/cyklista/164
Offline
#105 27. 06. 2012 10:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úlohy o pohybu
↑ petrik_ch:
vždyť je opět stejný cyklista :-)
Vážně - včera jsem se trochu dívala na projekt a chtěla jsem přidat odkaz na místní MatWiki, ale nějak jsem se nezorientovala ještě kam.
Je to určitě zajímavý nápad a užitečný. Jen bych měla (pokud mohu :-) připomínku - v řešeních není uváděno označení jednotlivých používaných neznámých (proměnných), pro ZŠ je dost nepřehledné, ještě není zkušenost. Např. zde je to opravdu obtížné se zorientovat. případně mít jeden odkaz s obrázkem na standardní značení v trojúhelníku, co se používá pro celou sbírku.
Jinak se zkuste porozhlédnout po fóru - myslím, že samostatné téma v Ostatním by mohlo mít větší odezvu. Děkuji.
Ať se daří.
Offline
#106 13. 07. 2012 22:20
#107 13. 07. 2012 23:02
#108 20. 07. 2012 10:40
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 242
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: slovní úlohy o pohybu
↑ jelena:
Ahoj jelena;
zbierku prikladov www.hackmath.net som zacal robit najma preto aby som ako tridsiatnik este nieco z matematiky si zopakoval. Urcite mate pravdu ze pre ziaka ZS to je asi dost neprehladne, najma zlozitejsie priklady. Na druhu stranu ani papierove klasicke zbierky prikladov obsahuju len vysledok. Ale beriem to ako vyzvu na skvalitnenie rieseni prikladov.
To ze sa priklad zda ze je to rovnaky "cyklista". Ale v skutocnosti je kazdy priklad unikatny. T.j. veduci na iny vysledok. Dost ma v praxi zaraza, ze na skolach sa prilis glorifikuje moc algebry. Tj. riesia sa abstraktne problemy a vysledkom je takmer nic nehovoriaci zlozity vzorec. V praxi su vsetky riesenia pozadovane numericky a postupnym sledom medzivypoctov sa k vysledku dostanem ovela rychlejsie.
Pridat priklad si moze vyskusat kazdy:
http://www.hackmath.net/sk/pridaj-ulohu
Je to zatial dost nedokonale, nie je k tomu poriadny manual:) A poviem rovno - vytvorit priklad spolu s otestovanim, prepocitanim, vyladenim latexoveho riesenia, nahratim obrazka trva dobru polhodinu.
Offline
#109 20. 07. 2012 13:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úlohy o pohybu
↑ petrik_ch:
Pozdrav a děkuji. Už jsem navrhovala založit si samostatné téma, bylo by přehlednější.
Nejsem ani metodik, ani vyučující matematiky, ani ničeho jiného. Ale:
Na druhu stranu ani papierove klasicke zbierky prikladov obsahuju len vysledok.
Klasické učebnice a sbírky obsahuji vzorové úlohy.
To ze sa priklad zda ze je to rovnaky "cyklista". Ale v skutocnosti je kazdy priklad unikatny. T.j. veduci na iny vysledok.
:-) ve skutečnosti je to úloha na pohyb hmotného bodu, která se dá velmi dobře nastandardizovat (konec konců je to tak zapracováno v algoritmu výpočtu) :-)
Dost ma v praxi zaraza, ze na skolach sa prilis glorifikuje moc algebry. Tj. riesia sa abstraktne problemy a vysledkom je takmer nic nehovoriaci zlozity vzorec. V praxi su vsetky riesenia pozadovane numericky a postupnym sledom medzivypoctov sa k vysledku dostanem ovela rychlejsie.
"takmer nic nehovoriaci zlozity vzorec" hovoří hodně - výsledek vyjádřený symbolicky umožňuje sledovat vzájemnou souvislost jednotlivých proměnných, ověřit si správnost minimálně pomocí dosazování jednotek - kolegu zřejmě na ZŠ nenaučili, proto má potíž na VŠ.
Ano, pokud dokážou vyřešit alespoň krokově s mezivýpočty, tak i to je úspěch, ale nemělo by to být cíl výuky, snad (je to spíš ustupování a hledání kompromisů).
Pridat priklad si moze vyskusat kazdy:
Pravě proto je dobré mít jednotně zavedené označení pro nejčastěji používané úlohy (např. podrobné označení trojúhelníku).
Také jsem si všimla, že algoritmus řešení trojúhelníku používá sinovu/kosinovu větu i v pravoúhlém trojúhelníku (bez komentáře), což na ZŠ asi není použitelné.
A poviem rovno - vytvorit priklad spolu s otestovanim, prepocitanim, vyladenim latexoveho riesenia, nahratim obrazka trva dobru polhodinu.
To určitě a všechno okolo ještě déle - neberte, prosím, můj komentář jako kritiku, jen jako takové neodborné postřehy :-)
A už navrhuji pokračovat v samostatném tématu - viz standard.
Děkuji a zdar přeji.
Offline
#110 20. 07. 2012 17:48
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 242
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: slovní úlohy o pohybu
↑ jelena:
dakujem za reakciu; ja som "novacik" oproti Vam;) a zda sa aj odborne;)
Len taka kratka reakcia:
"takmer nic nehovoriaci zlozity vzorec"
Na tom tazisku polkruhu je symbolicky vypocet mozny len vdaka jednoduchosti tohto rovinneho utvaru. Vacsina realnych uloh z technickej praxe vedie su algebraicky neriesitelne ;)
K prikladu http://www.hackmath.net/sk/slovne-ulohy … ?tag_id=77
je nutne len vediet Pytagorovu vetu + co je sinus a kosinus uhla v pravouhlom 3uholniku. Ale cisto obecne je Pytagorova veta len specialnym pripadom kosinusovej vety;) ... Ja ako ucitel by som uznal aj riesenie SUS trojuholniku ze by to ziak nakreslil, odmeral chybajucu vysku a stranu a vypocital obvod a obsah....
Offline
#111 20. 07. 2012 22:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úlohy o pohybu
↑ petrik_ch:
:-) vyrobila jsem téma, ve kterém můžete s kolegy pokračovat. "Ať v tom není nepořádek". (c)
Offline