Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 12. 2011 17:11 — Editoval Andrejka3 (16. 12. 2011 18:05)
Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
Ahoj, narazila jsem na příklad, kde si vůbec nevím rady :(
Je to ale poslední příklad na svazy :)
Zadání: Dokažte, že každý distributivní svaz, lze vnořit do svazu 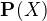 nějaké množiny
nějaké množiny  .
.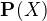 je zde svaz potenční množiny množiny
je zde svaz potenční množiny množiny  .
.
Prosím o pomoc,
A.
Edit: co je svaz, souvislost se svazovým uspořádáním jsem psala v prvním příspěvku tam.
Ve svazu 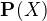 jsou operace
jsou operace 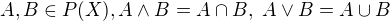 .
.
Tento svaz je distributivní.
Co je distributivita svazu jsem psala v prvním příspěvku zde.
Vnořením se myslí prostý homomorfismus.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#3 17. 12. 2011 12:38
Re: Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
↑ Olin:
:D Díky. Tak to odložím na pár desetiletí. Možná se k tomu ve svém životě ještě vrátím a vzpomenu si na toto založené téma.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 16. 01. 2012 02:40 — Editoval constr (16. 01. 2012 03:20)
Re: Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
↑ Andrejka3:snad nebude tak zle :-)
V originálním článku
 lze rozložit v subdirektní součet subdirektně nerozložitelných algeber z téže primitivní třídy, do níž patří algebra
lze rozložit v subdirektní součet subdirektně nerozložitelných algeber z téže primitivní třídy, do níž patří algebra  .
.Distributivní svazy tvoří primitivní třídu univerzálních algeber (varietu algeber), proto: Každý distributivní svaz je subdirektním součtem subdirektně nerozložitelných distributivních svazů.
Subdirektně ireducibilní distributivní svaz
 je svaz skládající se z nuly a jednotky svazu. Distributivnost svazu
je svaz skládající se z nuly a jednotky svazu. Distributivnost svazu  je zřejmá, protože byl by-li svaz
je zřejmá, protože byl by-li svaz  subdirektně ireducibilní, musel by být podsvazem úplného direktního součtu svazů
subdirektně ireducibilní, musel by být podsvazem úplného direktního součtu svazů  , přičemž by existovaly homomorfismy
, přičemž by existovaly homomorfismy 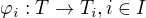 , jež by nebyly izomorfismy. Avšak potom by každý svaz
, jež by nebyly izomorfismy. Avšak potom by každý svaz  musel obsahovat pouze jediný prvek, a tedy i úplný direktní součet by byl jednoprvkový svaz a nemohl by existovat svaz
musel obsahovat pouze jediný prvek, a tedy i úplný direktní součet by byl jednoprvkový svaz a nemohl by existovat svaz  .
.Je každý subdirektně ireducibilní distributivní svaz, který obsahuje alespoň dva prvky, je izomorfní se svazem
 (?)
(?)Vezměme subdirektně ireducibilní distributivní svaz
 obsahující alespoň dva různé prvky. Skládá-li se
obsahující alespoň dva různé prvky. Skládá-li se  právě ze dvou prvků, je zřejmě izomorfní s
právě ze dvou prvků, je zřejmě izomorfní s  (z předchozího odstavce). Obsahuje-li
(z předchozího odstavce). Obsahuje-li  alespoň 3 prvky, je možno nalézt prvek
alespoň 3 prvky, je možno nalézt prvek 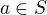 různý od nuly i jednotky svazu
různý od nuly i jednotky svazu  , pokud tyto prvky v
, pokud tyto prvky v  vůbec existují (!). Označme ještě
vůbec existují (!). Označme ještě  podsvaz všech prvků
podsvaz všech prvků 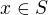 , pro něž platí
, pro něž platí 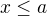 a
a  podsvaz všech takových
podsvaz všech takových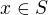 , že
, že 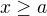 . Z předpokladů o svazu
. Z předpokladů o svazu  a prvku
a prvku  plyne, že každý z podsvazů
plyne, že každý z podsvazů  ,
, obsahuje mimo
obsahuje mimo  ještě alespoň jeden prvek.
ještě alespoň jeden prvek.Označme
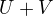 direktní součet svazu
direktní součet svazu  a
a  v následujícím smyslu (který explicitně napíšu, protože obsahuje princip užitý v závěru důkazu):
v následujícím smyslu (který explicitně napíšu, protože obsahuje princip užitý v závěru důkazu):Nechť je dána libovolná množina univerzálních algeber s touž množinou operací
 , jež všechny patří do téže variety algeber
, jež všechny patří do téže variety algeber 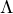 index
index  nechť probíhá množinu
nechť probíhá množinu  , jež může být konečná i nekonečná.
, jež může být konečná i nekonečná.Nechť
 je množina, jejíž prvky jsou všechny soustavy
je množina, jejíž prvky jsou všechny soustavy  prvků patřících po jednom do každé z algeber
prvků patřících po jednom do každé z algeber 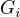 , tj.
, tj. 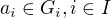 . Prvek
. Prvek  se nazývá i-tá komponenta (komponenta v algebře
se nazývá i-tá komponenta (komponenta v algebře 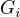 ) prvku
) prvku  . Z množiny
. Z množiny  utvoříme univerzální algebru s množinou operací
utvoříme univerzální algebru s množinou operací  tak, že operace z
tak, že operace z  definujeme po komponentách: je-li dána n-ární operace
definujeme po komponentách: je-li dána n-ární operace 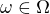 a n-tice prvků z
a n-tice prvků z 
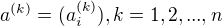 ,
, položíme
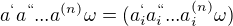 .
.Tak jsou splněny všechny identity z
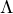 . Konečně, algebra
. Konečně, algebra  se nazývá direktním součtem algeber
se nazývá direktním součtem algeber  a značí se:
a značí se: (v odkazech, které jsem uvedl)
(v odkazech, které jsem uvedl)Vraťme se k původnímu důkazu, tedy nechť
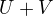 značí direktní součet svazů
značí direktní součet svazů  a
a  , tj. prvky součtu
, tj. prvky součtu 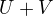 jsou dvojice
jsou dvojice 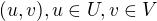 a operace s nimi se provádějí po komponentách (jak jsem uvedl výše). Přiřaďme každému prvku
a operace s nimi se provádějí po komponentách (jak jsem uvedl výše). Přiřaďme každému prvku 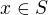 v distributivním svazu
v distributivním svazu  dvojici
dvojici 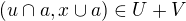 . Toto zobrazení
. Toto zobrazení  do
do 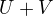 je injektivní, protože v distributivním svazu
je injektivní, protože v distributivním svazu  pro libovolné dva prvky
pro libovolné dva prvky 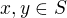 takové, že
takové, že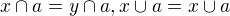 plyne
plyne  .
.Toto zobrazení je dokonce bijektivní resp. izomorfismus, protože:
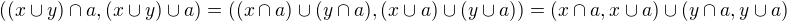
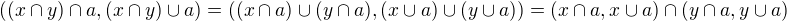 .
.Je tedy možno považovat
 za podsvaz svazu
za podsvaz svazu 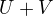 . Protože prvku
. Protože prvku 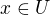 odpovídá dvojice
odpovídá dvojice 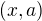 a prvku
a prvku 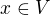 dvojice
dvojice 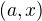 , zobrazují homomorfismy, přiřazující každému prvku z
, zobrazují homomorfismy, přiřazující každému prvku z  jeho první, resp. druhou složku, svaz
jeho první, resp. druhou složku, svaz  na celé
na celé  , resp. na celé
, resp. na celé  a přitom nejsou nejsou izomorfismy. To znamená, že
a přitom nejsou nejsou izomorfismy. To znamená, že  je subdirektně rozložitelný svaz, což je spor s původním tvrzením (s otazníkem :-) ).
je subdirektně rozložitelný svaz, což je spor s původním tvrzením (s otazníkem :-) ).Odtud pak uvažme libovolný distributivní svaz
 ; to znamená, že
; to znamená, že  je subdirektním součtem svazů
je subdirektním součtem svazů  , kde každý svaz
, kde každý svaz 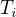 se skládá právě ze dvou prvků, ze své nuly
se skládá právě ze dvou prvků, ze své nuly  a jednotky
a jednotky 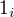 . Symbolem
. Symbolem  označme množinu všech jednotek
označme množinu všech jednotek 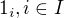 a přiřaďme každému prvku
a přiřaďme každému prvku 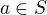 podmnožinu
podmnožinu  všech těch jednotek
všech těch jednotek 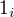 , jež se vyskytují jakožto i-té komponenty prvku
, jež se vyskytují jakožto i-té komponenty prvku  , chápaného jako prvek úplného direktního sousčtu svazů
, chápaného jako prvek úplného direktního sousčtu svazů  . Je jasné, že pro
. Je jasné, že pro 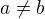 budou i jim odpovídající podmnožiny různé. z toho, že operace v úplném direktním součtu svazů
budou i jim odpovídající podmnožiny různé. z toho, že operace v úplném direktním součtu svazů  , se definujípo komponentách (jak jsem uvedl!), a z vlastnosti jednotky a nuly svazu ihned plyne, že
, se definujípo komponentách (jak jsem uvedl!), a z vlastnosti jednotky a nuly svazu ihned plyne, že 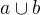 prvků z
prvků z  odpovídá sjednocení
odpovídá sjednocení 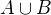 příslušných podmnožin a průseku
příslušných podmnožin a průseku 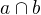 průnik
průnik 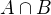 . Tím je úloha vyřešena.
. Tím je úloha vyřešena.Řešení lze zkrátit pomocí termínů Booleových svazů.
Booleův svaz (Booleova algebra) je svaz s nulou a jednotkou, když pro každý prvek
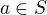 existuje komplement
existuje komplement 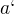 , pro nějž platí
, pro nějž platí  a
a 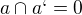 a
a  .
.Tato "komplementace" je jednoznačná.
Svaz všech podmnožin libovolné množiny
 je Booleovým svazem, neboť ke každé podmnožině
je Booleovým svazem, neboť ke každé podmnožině  existuje množinový komplement
existuje množinový komplement  . Množinový svaz, který obsahuje s libovolným svým prvekm i jeho doplněk je Booleův množinový svaz.
. Množinový svaz, který obsahuje s libovolným svým prvekm i jeho doplněk je Booleův množinový svaz.Odpovídá-li prvku
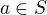 podmnožina
podmnožina 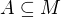 , je jeho komplementu
, je jeho komplementu 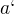 přiřazen množinový komplement
přiřazen množinový komplement 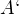 podmnožiny
podmnožiny  v
v  . To však ihned plyne z toho, že vyjádření prvků
. To však ihned plyne z toho, že vyjádření prvků  a
a 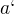 v úplném direktním součtu svazů
v úplném direktním součtu svazů  jsou taková, že má-li jeden z nich i-tou komponentu rovnou
jsou taková, že má-li jeden z nich i-tou komponentu rovnou 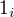 , je u druhého rovna
, je u druhého rovna  a naopak.
a naopak. ↑ Olin:
Takovým věcem bych rád někdy rozuměl...
Poznámku: pěkně je téma zpracováno v Kurošových "Kapitolách z obecné algebry", je tam spoustu dalších zajímavých témat.
s pozdravem Honza
Offline
#5 15. 02. 2012 02:03 — Editoval Andrejka3 (15. 02. 2012 02:05)
Re: Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
Chtěla bych Vám velice poděkovat za tak vyčerpávající odpověď. Zároveň se omlouvám, že mi to tak dlouho trvalo. Celou věc si podrobně projdu.
Edit: Nějakou dobu jsem neměla sílu zabývat se pořádně matematikou. Tohle by mě mohlo vzpružit :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 15. 02. 2012 15:17 — Editoval Andrejka3 (15. 02. 2012 15:21)
Re: Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
Nerozumím některým pojmům.
Takhle si to představuji...
Direktní součet (univerzálních) algeber:
Projekce na direktním součinu:
Definice subdirektního součtu pracuje s pojmem inkluze.
Subdirektní součet:
Myslí se tady inkluzí libovolný prostý homomorfismus
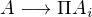 ? Nebo to je jen toto zobrazení:
? Nebo to je jen toto zobrazení: 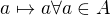 ? Je-li
? Je-li  vlastní podalgebrou
vlastní podalgebrou  , existuje vždy
, existuje vždy 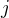 takové, že
takové, že 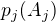 je vlastní podalgebrou
je vlastní podalgebrou 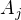 ? Je každý direktní součet též subdirektním?
? Je každý direktní součet též subdirektním?Mám v tom zmatek a představit si dubdirektní součet mi dělá problém. Děkuji za každou radu.
Osobní pozn.:
Edit: Téma je sice vyřešené, ale já to pořád nechápu, přes snahu kolegů. Dovolím si to označit za nevyřešené, protože vyřešenost tématu se má vztahovat k tomu, jestli zadavatel chápe řešení, ne?
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 12. 12. 2013 17:52
Re: Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny
Tady je idea dukazu (konstrukcniho) pro konecne distributivni svazy: http://forum.matweb.cz/viewtopic.php?id=68016
Prispevku ↑ constr: jeste chvili rozumet nebudu.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Distributivní svaz lze vnořit do svazu všech podmnožin nějaké množiny (TOTO TÉMA JE VYŘEŠENÉ)

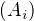 nejvýše spočetný soubor (univerzálních) algeber stejného typu. Definujeme
nejvýše spočetný soubor (univerzálních) algeber stejného typu. Definujeme 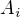 a operace jsou definovány po složkách.
a operace jsou definovány po složkách.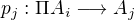 definované předpisem
definované předpisem  , jemuž říkáme projekce j-té složky.
, jemuž říkáme projekce j-té složky. inkluze, pak zobrazení
inkluze, pak zobrazení  je surjekce
je surjekce 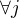 .
.