Matematické Fórum

Blujacker

Ahoj,

Při derivacích jsem narazil na menší problém. Jedná se o příklad $y=\sqrt[3]{\frac{1+x^3}{1-x^3}}$
Postupoval jsem následovně:
$y'=\frac{1}{3}\left(\frac{1+x^3}{1-x^3}\right)^{(-\frac{2}{3})}*\frac{(1+x^3)'*(1-x^3)-(1+x^3)*(1-x^3)' }{(1-x^3)^2}\nly=\frac{1}{3}\left(\frac{1+x^3}{1-x^3}\right)^{(-\frac{2}{3})}*\frac{6x^2}{(1-x^3)^2}=\left(\frac{1+x^3}{1-x^3}\right)^{(-\frac{2}{3})}*\frac{2x^2}{(1-x^3)^2}$
Nyní nevím jak zjednodušit tu prví část výsledku. Myslím, že platí $x^{\frac{a}{b}}=\sqrt[b]{x^a}$ a tím pádem by výsledek byl $y'=\sqrt[3]{\left(\frac{1-x^3}{1+x^3}\right)^2}*\frac{2x^2}{(1-x^3)^2}$ .

Jenomže moje učebnice říká něco jiného. Lišíme se v tom, jak se zbavit toho 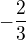$-\frac{2}{3}$ . Jejich řešení vypadá takto:

Je možné že v tom mají chybu, anebo jsem něco nepochopil já?

Děkuji

PS: zkoušel jsem použít kalkulátor, ale jejich program začínal derivací podílu místo řetězového pravidla.

O.o · 14. 02. 2009 01:46 — Editoval O.o (14. 02. 2009 01:51)

↑ Blujacker:

$\left(\frac{1+x^3}{1-x^3}\right)^{- \frac{2}{3}} = \left(\frac{1-x^3}{1+x^3}\right)^{\frac{2}{3}} = \sqrt[3]{ \left (\frac{1-x^3}{1+x^3} \right)^2} = \sqrt[3]{\frac{1+x^3}{1-x^3} \cdot \left(\frac{1-x^3}{1+x^3}\right)^3} = \sqrt[3]{\frac{1+x^3}{1-x^3}}\cdot\frac{1-x^3}{1+x^3}$

Je to t, co hledáš? Mne to v tuhle hodinu moc nemyslí a už ani nevidím na monitor, jestli jsem se tedy někde zpletl, budu rád, když mne někdo opraví (moc jsem to nekontroloval, jen psal v texu, tak doufám ,že jsem si správně zapamatoval ten původní zlomek)..

PS: Takhle mi nepřijde, že se moc s učebnicí lišíte .)..

Blujacker · 14. 02. 2009 01:55

Nechápu tu úpravu. Jak se z $\sqrt[3]{\left(\frac{1-x^3}{1+x^3}\right)^2}$ stane $\sqrt[3]{\frac{1+x^3}{1-x^3}\cdot \left(\frac{1-x^3}{1+x^3}\right)^3}$

O.o · 14. 02. 2009 02:20 — Editoval O.o (14. 02. 2009 02:21)

↑ Blujacker:

$\sqrt[3]{\frac{1+x^3}{1-x^3}\cdot \left(\frac{1-x^3}{1+x^3}\right)^3}=\sqrt[3]{\frac{\cancel{1+x^3}}{\cancel{1-x^3}} \cdot \frac{(1-x^3)^{\cancel{3}}}{(1+x^3)^{\cancel{3}}}} = \sqrt[3]{\frac{(1-x^3)^2}{(1+x^3)^2}}$

Proč se to dělalo, napadá mne jen proto, že čitatel jednoho zlomku a jmenovatel druhého jsou stejní (dalo by se nějak krátit? Nevím, tak zkusím něco, jestli by to nešlo .)), já jsem na ty úpravy úplně levý, tak mne jiný důvod nenapadá..

PS: Jedna možnost by také byla, abys to krátil rovnou (tím myslím tu část, která vyšla tobě) a upravoval dál..

halogan · 14. 02. 2009 09:48

Protože ten první zlomek si můžete napsat jako na minus prvou a pak sečíst mocnitele -1 + 3 = 2.

kaja.marik · 14. 02. 2009 14:56

↑ O.o:
Mozna autorovi pripadlo pekne, ze se z toho vyloupne puvodni zadani krat neco.
Neni proste presne dane, do jakeho tvaru to upravit. Z urciteho uhlu pohledu je lepsi mit upravy treba takto, nekdo jiny to preferuje jinak.
Hlavni je ze derivace vysly v obou pripadech stejne.
A mozna ze kdyby se clovek zeptal puvodniho autora tak sam uz nebude vedet, proc to upravoval prave takto ..... :)

Blujacker · 14. 02. 2009 17:22

↑ halogan:
Děkuji, už to chápu

Mám ještě několik nejasností co se týče derivací. Pokud mám například funkci $\frac{\sin x\cdot\ln x}{x^2}$ , tak začnu derivovat nejdříve podíl nebo ten součin v čitateli?

Přečetl jsem si, že pro funkci $f(x)=e^x$ je derivace $f'(x)=e^x$ . Čekal bych tedy že $\frac{d}{dx}e^{\sqrt{x}}=e^{\sqrt{x}}$ . Opět se rozcházím z výsledky.

Je to dobře, či špatně?

Děkuji

jelena · 14. 02. 2009 17:30

↑ Blujacker:

Zdravím :-)

1. začneš derivovat podíl (řekla bych, že derivujeme zpět od poslední operace)

2. $(e^{\sqrt{x}})^\prime=e^{\sqrt{x}}\cdot (\sqrt{x})^\prime=...$

zde už máme derivaci složené funkce. OK?

halogan · 14. 02. 2009 17:32

↑ Blujacker:

$e^{\sqrt{x}}$ se derivuje jako složená funkce.

$(e^{\sqrt{x}})' = e^{\sqrt{x}} \cdot (\sqrt{x})'$

Co se týče toho $\frac{\sin x \cdot \ln x}{x^2}$

Ze vzorce na derivaci podílu budete muset stejne derivovat jak součin, tak podíl. Tak si udělejte bokem derivaci součinu a pak to zakomponujte do podílu.

Blujacker · 14. 02. 2009 17:41

↑ jelena:
Děkuji

Ještě snad pro jistotu, platí tedy:
$(\sin x^{\sqrt{x}})'=\sin x^{\sqrt{x}}\cdot(\sqrt{x})'$

halogan · 14. 02. 2009 17:44

↑ Blujacker:

Ne, ten sinus musíš zderivovat. Tedy $\cos x^{\sqrt{x}} \cdot \textrm{...}$

jendula11 · 14. 02. 2009 18:09

↑ Blujacker:no na toto by se podle měly použít logaritmické derivování

jelena · 14. 02. 2009 18:42

Zdravím vás :-)

ještě takové poznámky - v zadání s ln možna by se hodila hned na úvod úprava (nebo na závěr):

$\sqrt{\ln(\text{e}^{sqrt{x}})} =\sqrt{\sqrt{x}\ln\text{e}}=...$

v zadání se sin (doplním závorky) - je to tak myšleno?

$(\sin (x^{\sqrt{x}}))'=(\cos (x^{\sqrt{x}}))\cdot(x^{\sqrt{x}})'$

a tato část se má derivovat pomocí logaritmického derivování

$(x^{\sqrt{x}})'$

V nasledujících odkazech jsou prezentovány názorové rozdily účastniků fóra - zastanců jednotlivých metod:

http://forum.matweb.cz/viewtopic.php?id=1687

http://forum.matweb.cz/viewtopic.php?id=4871

http://forum.matweb.cz/viewtopic.php?id=228

a záznam vzniku Saturdayova vzorce:

http://forum.matweb.cz/viewtopic.php?id=2192

to jen tak, na doplnění, vysvětlení od kolegovů halogan a jendula11 je zcela dostačující.

Matematické Fórum

#1 14. 02. 2009 01:30 — Editoval Blujacker (14. 02. 2009 01:31)

Derivace funkce

#2 14. 02. 2009 01:46 — Editoval O.o (14. 02. 2009 01:51)

Re: Derivace funkce

#3 14. 02. 2009 01:55

Re: Derivace funkce

#4 14. 02. 2009 02:20 — Editoval O.o (14. 02. 2009 02:21)

Re: Derivace funkce

#5 14. 02. 2009 09:48

Re: Derivace funkce

#6 14. 02. 2009 14:56

Re: Derivace funkce

#7 14. 02. 2009 17:22

Re: Derivace funkce

#8 14. 02. 2009 17:30

Re: Derivace funkce

#9 14. 02. 2009 17:32

Re: Derivace funkce

#10 14. 02. 2009 17:41

Re: Derivace funkce

#11 14. 02. 2009 17:44

Re: Derivace funkce

#12 14. 02. 2009 18:09

Re: Derivace funkce

#13 14. 02. 2009 18:42

Re: Derivace funkce

Zápatí